目次
『熊野コミチの「ものづくり統計学」』では、メーカーの製品開発者が、ものづくりのための統計学をテーマに、実際に現場で統計学を使う際のポイントや罠、現実などを普段活用している立場から解説します。
記事一覧:【連載】熊野コミチの「ものづくり統計学」

皆さんこんにちは。熊野コミチです。
モノづくりのための統計学、第5回は「箱ひげ図の外れ値、その発生する確率は?」です。
読者の皆さんは、箱ひげ図って使っていらっしゃいますか? もし使ってないのだとしたらもったいないです。明日からでも使った方が良いです!
というのも、このような理由があるからです。
- 平均、ばらつき、外れ値といった複数の情報が一目で把握できる
- 分布の比較がヒストグラムより分かりやすい
なので、ラインAとラインBの品質って同等と言えるのかみたいな量産工程の層別分析において非常に強力な武器になります(図1)。
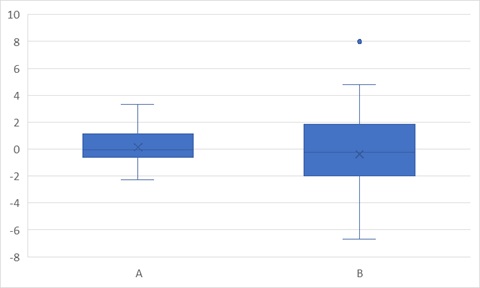
ちなみに、真ん中の×が平均値、箱のサイズがばらつき、箱から飛び出している棒が分布内の最大、最小値、棒から飛び出している点が外れ値(他の値よりかなり離れてポツンとあるような値)になります。
上記のグラフの場合だと、AとBは平均値は似ているのですが、箱のサイズがBの方が大きいのでBの方がばらつきが大きく、Aとは異なる分布になっていることが分かります。
そこまで詳細に言われるまでもなく、
「AとB明らかにグラフの形違うよなぁ」
というのは直感的に察することができるかと思います。変に検定などを使う必要もありません。(検定の危険性については第3回をご参照ください)。
さて、この箱ひげ図ですが、私は使い始めたときにこんなことを思いました。
「これ、上司から『外れ値ってどのくらいの確率で発生すんの』って言われたらどうしよう」
あなたが今、箱ひげ図を使っていない場合、それは職場にそのグラフが定着していないからだと思うんです。つまり職場で見かけないグラフなので、初めて使う場合はまずグラフそのものの説明をしなければなりません。
他のところ、箱の意味とかはネットで検索したらいくらでも出てきます。事前に予習が可能です。ただ「外れ値がどのくらいの確率で発生するのか」は検索しても見つかりません。底意地の悪い上司の場合、ちょっと言い淀んだだけで鬼の首を取ったかのように「そんなよく分かってない手法は使えない」とか言い出しかねません。
ということで今回は、箱ひげ図の外れ値の発生確率について考えてみましょう。
箱ひげ図の外れ値の発生確率はどうすれば分かる?
最初に断っておきます。箱ひげ図の外れ値が出る確率を知ることは不可能です。
「分かった、じゃあね、あばよ」
あ、ちょっと、待ってぇ!
待ってください~~!
言い訳を……、言い訳をする時間を私にください! 箱ひげ図の外れ値を想定できない理由は、そもそも箱ひげ図が分布を仮定とした手法ではないからなんです。
箱ひげ図の外れ値は箱のサイズ(IQRといいます)の1.5倍を箱の上に乗せて、そこから外れる範囲を外れ値としようとするものです。
つまり、「分布からこのくらい離れてたら外れ値と良いのでは?」というのが、箱ひげ図の外れ値の決め方なります。そのような決め方でないと、分布を仮定としていない場合外れ値を想定することは難しいですから。
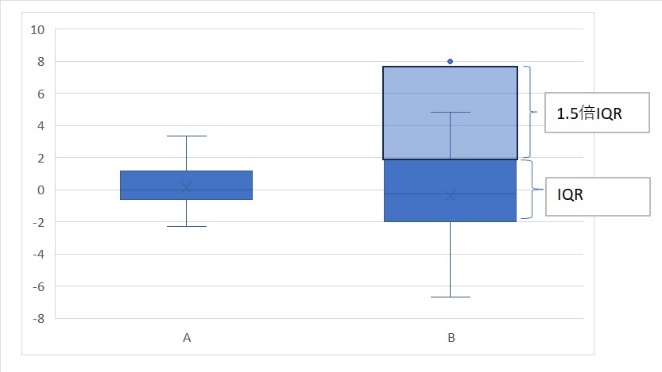
ただこのような説明では、なかなか上の納得を得るのは難しいかと思います。という事でここからは正規分布を箱ひげ図で表現した場合に、外れ値が発生する確率という観点で考えてみたいと思います。
そうであれば、「箱ひげ図の外れ値は、もしデータが正規分布をしている場合は~%の確率で発生します。そのようなイメージで発生するものなんだとお考え下さい」という一応の説明は立つかと思います。
正規分布と想定すると、どうなる?
ということで、ここからは「正規分布だった場合」という過程で考えていくのですが、どこをとっかかりにしましょうか。
ここでは四分位数をとっかかりにして考えいきましょう。というのも、四分位数はデータの中心(中央値)から何%離れた箇所という区切りのつけ方をするので、確率分布とグラフをつなげる接点になるからです。
まず四分位数から簡単に説明します。四分位数とはデータを小さい順に並べて、そのデータ群を4分割する3つの数字になります(図3)。

| 名称 | 説明 | 図3での位置/値 |
|---|---|---|
| 第一四分位数 | データ群の下から25%の位置にある数字 | No. 4/57 |
| 第二四分位数 (中央値) | データ群の下から50%の位置にある数字。 中央値ともいう | No. 7 と No. 8 の間/62 |
| 第三四分位数 | データ群の下から75%の位置にある数字 | No. 11/73 |
この第1四分位数と第3四分位数が正規分布の場合はどのような確率変数Xになるのかを考えれば、箱のサイズが見えてきて最終的に外れ値がどのくらいの確率で出るのかが分かるわけです。
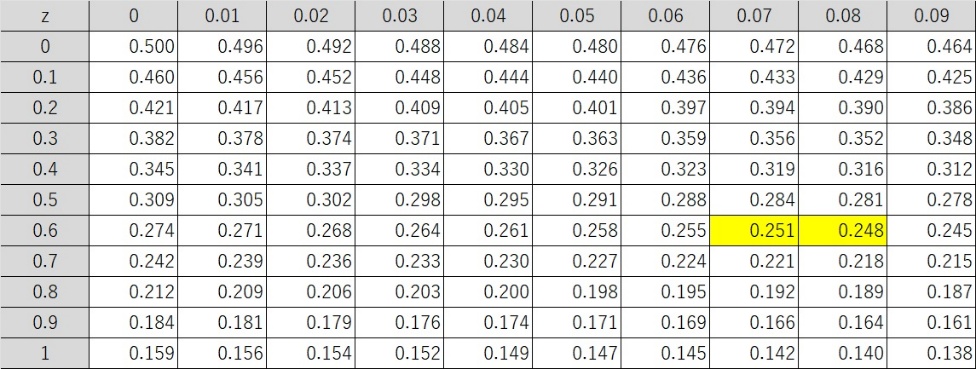
正規分布の中央から25%離れた場合の確率変数は何になるのか、正規分布表で確認してみましょう(図4)。
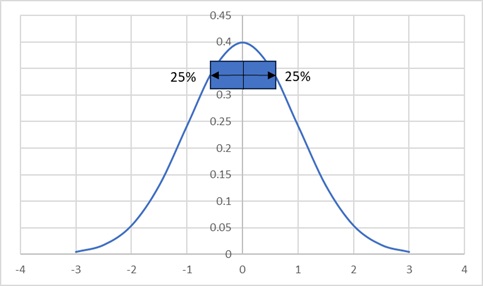
図5より、確率変数z=0.67~0.68が大体25%(=0.25)の点になりそうです。Excelで計算したら、zは約0.675でした。そして箱のサイズはこの確率変数の倍になりますので、0.675×2=1.35になります。
箱ひげ図の外れ値は、箱の上端(もしくは下端)に1.5倍した箱のサイズを乗せてそこから外れた値になります。
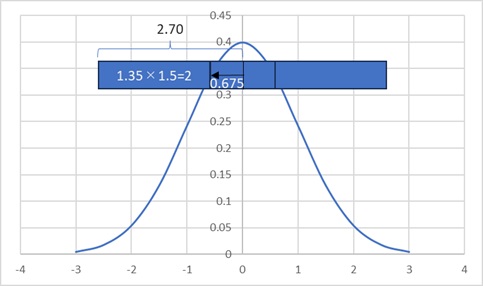
0.675+1.5×1.35≒2.70
つまり平均値0から2.7σ外れると、箱ひげ図の外れ値と一致するわけです。
さてこの2.7σですが、正規分布における外れ値とされる3σに結構近い値ですよね?
なので私はこれを初めて算出した時「案外妥当なんかな」という感想を抱きました。ちなみに2.7σから外れる確率は、0.7%くらいです(3σ外れの確率は0.3%)。
外れ値について突っ込まれても大丈夫!
正規分布を箱ひげ図で描画した場合、外れ値が発生する確率は0.7%程度だということが分かりました。
なので、もし上司から、
「ふーん、この箱ひげ図ってやつの外れ値はどのくらいの確率で発生するの?」
と聞かれたら、
「正規分布の場合だと大体0.7%くらいの確率で外れ値が発生します。なのでそのくらいの温度感でこのグラフを眺めてもらえれば良いかと」
という感じで答えられます。やりましたね!
ちなみにそもそも箱ひげ図のこととか、四分位数とかのことが、最初から全く分からないという場合は、私のYouTubeチャンネルをご覧ください。箱ひげ図について最初から丁寧に解説しています。その動画を見た後にこちらの記事に戻っていただければ理解度も増すかと思います。
関連リンク:これで見方が分かる! 箱ひげ図|統計とお仕事チャンネル(YouTube)
記事一覧:【連載】熊野コミチの「ものづくり統計学」
参考文献
本当にわかりやすいすごく大切なことが書いてあるごく初歩の統計の本 吉田寿夫・著(北大路書房)
執筆者プロフィール
熊野コミチ
メーカーで製品開発に従事。過去には品質管理・保証業務で統計を使った工程管理や分析を経験。仕事で使える統計学をテーマに、最近では品質工学、品質管理、実験計画法などをYouTubeなどで情報発信している。
ただ単に聞きかじった教科書的な知識ではなく、実際に実用し失敗したりうまくいったりした経験から得たポイントや、“現場で使える”ノウハウを強みとして発信を続けている。登録者数は1万7000人を超える。
執筆者サイト、SNS




