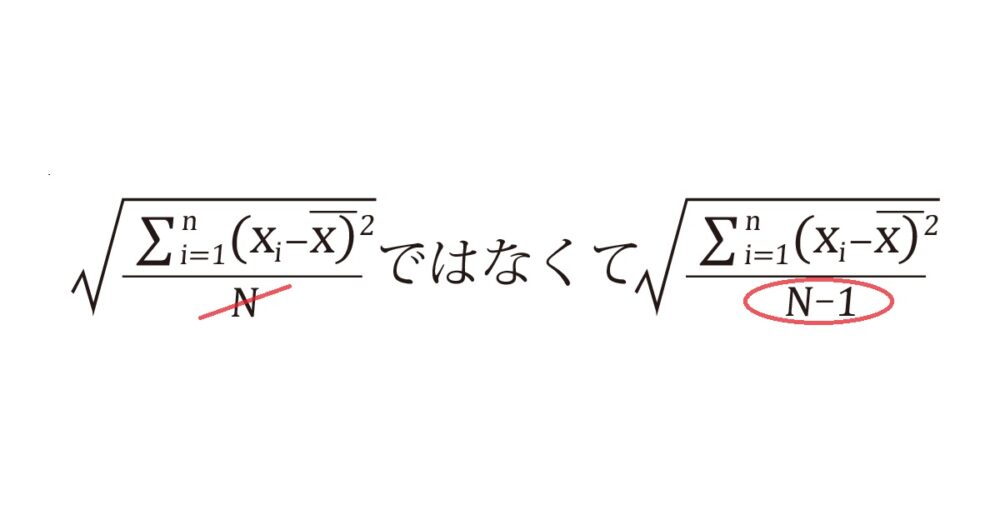『熊野コミチの「ものづくり統計学」』では、メーカーの製品開発者が、ものづくりのための統計学をテーマに、実際に現場で統計学を使う際のポイントや罠、現実などを普段活用している立場から解説します。
記事一覧:【連載】熊野コミチの「ものづくり統計学」

皆さんこんにちは。熊野コミチです。
モノづくりのための統計学、第4回は「標準偏差N-1で割る理由」というお話をしたいと思います。
QCや統計学を学び始めると、最初のあたりで標準偏差につい学習することになるかと思います。そしてこういう解説を聞くことになります。
「採取したサンプルから母数を推定するために、NではなくN-1で割りましょう」
(不偏標準偏差のときは、N-1で割る)
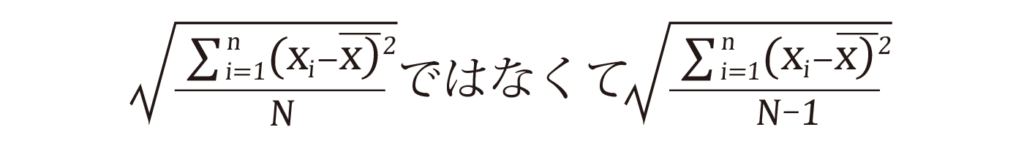
これ納得できますか? 私はすごく気になりました。なんか喉に骨が引っかかっているような感じです。確かにここの部分をちゃんと理解していないと使えないということはないです。
「推測統計の時はN-1で割るんだな」という理解だけで、全然OKです。ただどうしてもその理由が気になるなぁという方だけ、今回の記事をお読みいただければと思います。
なぜ補正が必要なのか?
「N-1で割る」というのは、つまり補正です。この補正がないと母数(真の標準偏差)を推定できないのです。ということで、まずは「なぜ補正が必要なのか」というところから考えていきましょう。
この問題を考えるにあたって、以下の性質を知っておく必要があります。
「算術平均から偏差の平方和は、他のいかなる一定値からの偏差の平方和よりも小である」
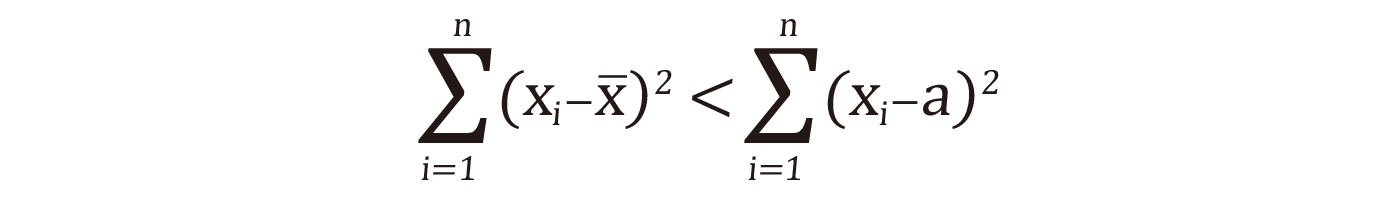
これが、補正が必要な理由です。算術平均はこの場合、母集団から採取した際のサンプルの平均値に該当します。そして他のいかなる一定値というのが、今回の場合、母集団そのものの平均値μになります。
皆さんも感覚的に、サンプリングした標本の平均値と母集団の平均値は一致しないことが多いというのは理解できると思います。この平方和Nで割ったものの平方根が標準偏差になるのですから、
結局、このような関係が成立します。
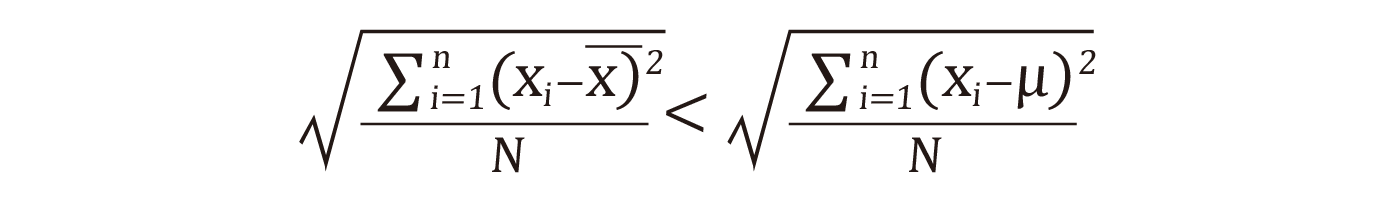
という関係が成立します(一定値aを母集団の平均値μに置き換えています)。
つまり標本の平均値が母集団の平均値と一致した場合(x̄=μ)を除き、標本の平均値を使って算出される標準偏差は、母集団の標準偏差よりも小さくなってしまうわけです。故に何かしらの補正をして、母集団の標準偏差を推定してあげる必要が出てきます。
それでは、どういう補正を行うか?
さて、ここでどういう補正を行うかです。そもそも標本の標準偏差が小さくなるということは、母集団の標準偏差と比べて何かのばらつきが欠けているということを指します。つまりその欠けているものを加えれば良いわけです。
その欠けているものとは、平均値のばらつきです。
皆さんも経験的にご存じだと思いますが、標本の平均値は採取するたびにばらつきます。一方母集団の平均値は一定です。つまり標本の標準偏差が小さくなるのは、この標本の平均値のばらつきが抜けているからに他なりません。
ちなみに平均値のばらつきは、母集団の標準偏差を√nで割った値です(中心極限定理より)。
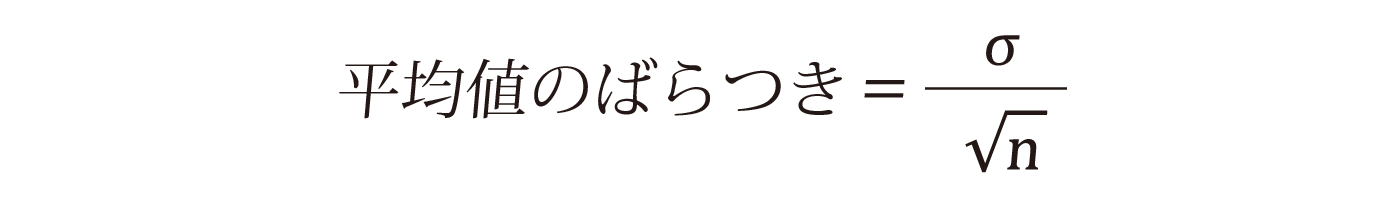
なおσは母集団の標準偏差を指します。
以下sを標本の標準偏差、σを母集団の標準偏差として話を進めます。
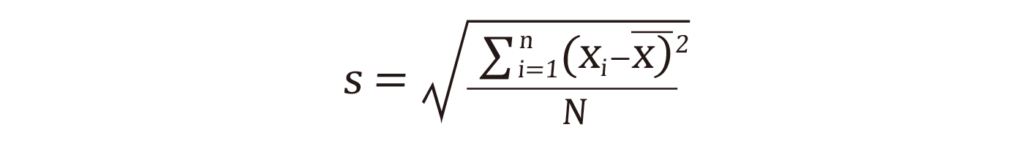
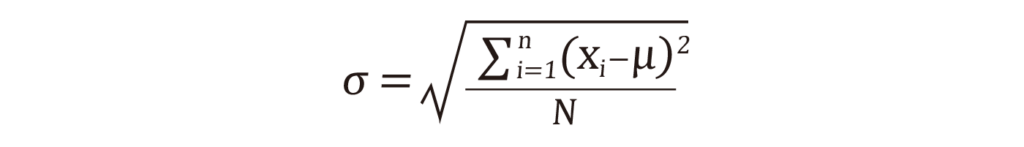
また計算過程を容易にするために、分散(標準偏差の二乗)で計算を進行します。
さて、「標本の標準偏差に平均値のばらつきを加えて補正する」ということを式で表現すると、こうなります。
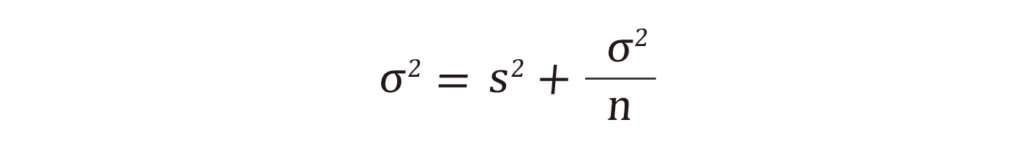
左辺が母集団の分散、右辺第一項が標本の分散、第二項が標本の平均値の分散です。
これを変形すると、
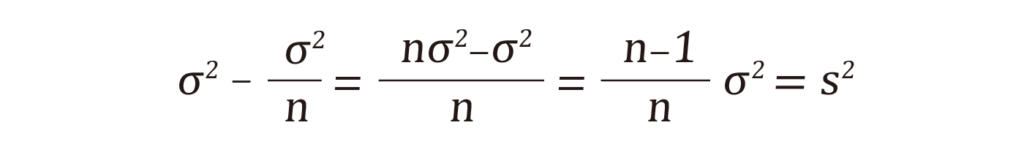
つまり、母集団の分散をn-1/n倍したものが標本の分散と一致するわけです。
ここからさらに変形すると、
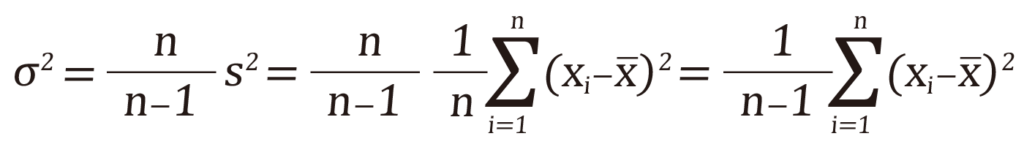
このように、標本の分散にn/n-1をかけると母集団の分散に一致します。つまりそれらの平方根をとった標準偏差も同様に一致するわけです。
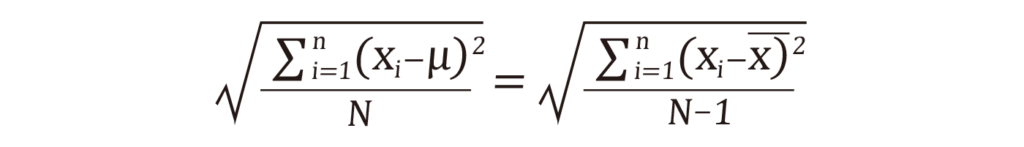
ということで、これが標準偏差をN-1で割る理由になります。
標準偏差の関数も、標本か母集団かで違う
ということでN-1で割ることで、母集団の標準偏差を推定することができます。とは言っても、今時は手計算ではなくExcelで算出するほうがメインだと思うので、あまり気にする機会はないかもしれませんね。ただExcelも標準偏差の関数は複数存在しており、これらを誤って使ってしまう可能性もありますので、あらためてExcelの関数の紹介もしておきます。
- STDEVもしくはSTDEV.S:標本から母数を推定する標準偏差関数(N-1で割る方)
- STDEV.P:集団そのものの標準偏差関数(Nで割る方)
品質管理では基本的に未知である母数の推定を前提とするので、N-1の方であるSTDEV.Sをメインで使うことになります。間違ってSTDEV.Pを使わないように注意しましょう。
一方。品質工学で「MT法」という手法があるのですが、その際は単位空間というサンプリングした集団そのもののばらつきが重要になるので、Nで割る方のSTDEV.Pを使用します。 要はシチュエーションによって、関数の使い分けが必要になるので、N-1で割る理由は忘れても、どのような目的でどちらの関数を使うのかは認識しておきましょう!
関連リンク:熊野コミチ 統計とお仕事チャンネル(YouTube)
記事一覧:【連載】熊野コミチの「ものづくり統計学」
参考文献
基本統計学 宮川 公男・著(有斐閣)
執筆者プロフィール
熊野コミチ
メーカーで製品開発に従事。過去には品質管理・保証業務で統計を使った工程管理や分析を経験。仕事で使える統計学をテーマに、最近では品質工学、品質管理、実験計画法などをYouTubeなどで情報発信している。
ただ単に聞きかじった教科書的な知識ではなく、実際に実用し失敗したりうまくいったりした経験から得たポイントや、“現場で使える”ノウハウを強みとして発信を続けている。登録者数は1万7000人を超える。
執筆者サイト、SNS