有意差検定は使うのやめとけ｜熊野コミチの「ものづくり統計学」【第3回】

皆さんこんにちは。熊野コミチです。
モノづくりのための統計学、第3回は有意差検定を使っちゃダメというお話をしたいと思います。

製造業でデータを扱っていると、

「平均値では5くらい違うけど、これってばらつきレベルか差があるのか分からんな？」

「改善アクションとったけど、ほんとに改善したのかな？」

「田中と鈴木のとったデータほんとに同じと言えるかな？」

など、要は「本当に差があるんかな？」ということを知りたい状況によく出くわします。

グラフで見比べても、「結局人によって見解違ってくるし、もっと良い方法ないのかな？」と困った人が統計学を学ぶと巡り合うのが、そう、「有意差検定」という手法です。

ASA「有意差検定を使うのやめときなさい」

私自身、4M変更で材料を変更する際に「これホントに同じ品質なのか」と詰められまくり、そのトラウマから必死に検定を勉強したことがあります。

このように一見すると、すごく有用そうな手法ではありますが、実は最近雲行きが怪しいのです。というのもアメリカ統計協会（ASA)が2016年に声明を出した（※）ことを皮切りに、「検定でデータの有意差を判断するのはやめた方がいい」という風潮になっているんです。

※ASAは「有意差検定やp値は仮説の正誤を直接判定するものではない」とし、p値や信頼区間などの統計的指標の意義は認めつつも、それらを唯一の基準として結論を出すことは誤解や社会的な害を招くリスクがあると警告した。
The ASA Statement on p-Values: Context, Process, and Purpose
https://www.tandfonline.com/doi/full/10.1080/00031305.2016.1154108

「とても便利そうなのにそりゃないよ」と言いたくなるかもですが、実際に検定を勉強していた僕自身、「あれこの手法ってホンマ大丈夫か？」という疑問を抱いていたので、このような声明や風潮があるという話を聞いたときに妙に納得したんですよね。実際に検定を使ってしまうと、間違った判断をしてしまう可能性があり、結構危険なので「今度検定を使おうとしてたんだよね」という方にはぜひここから先、検定を使っちゃダメな理由を学んでいっていただきたいです。

有意差検定とは何か

ここからは、以下のようなシチュエーションを元に、検定というものを考えていきましょう。

「硬度をアップさせるために改善アクションをとある設備に施した。実際に効果があるのか確認するために、実際にその設備でモノを作ってデータを取ってみた。グラフの上では差があるように見えるが、実際に改善できたという客観的な事実が欲しいので検定を実施してみることにした」

よくありそうな話ですよね。

今回の場合、改善前の硬度と改善後の硬度の平均値を比較することになると思います。今回はz検定を使ってみることにします。改善前のデータはたくさんあるので、平均値と標準偏差が結構な精度で分かっています。

＜改善前＞
硬度平均:10 硬度標準偏:0.5

改善後は、今回10個作って平均値を測定してみました。そうしたところ、以下の結果になりました。

＜改善後＞
硬度平均:12 サンプルサイズ:10

これらの値を使って検定を実施します。

検定の基本的な流れは以下の通りになります。

1. 帰無仮説を立てる
2. 対立仮説を立てる
3. 有意水準を設定する
4. 適切な検定統計量を決める
5. 検定統計量をもとに結論を決める

順を追って簡単に解説します。

まずは「帰無仮説」という「否定する前提の仮説（仮説を無に帰そうとする仮説）」を立てます。ここでは「改善前＝改善後」（改善前後で差はない）という帰無仮説になります。つまり「改善前と改善後の差として出てきた値は、単なる偶然であったと考えられる」ということを示します。

そしてその帰無仮説と対立する仮説を立てます。今回だと「改善前＜改善後」という対立仮説であり、「改善前後の差であると考えられる（偶然には極めて低い確率でしか起こり得ない）」ということを示します。

帰無仮説（推したい仮説を否定する仮説）を否定することで、対立仮説（推したい仮説）を採用する。これが検定の基本的な考え方です。 背理法の考え方と共通してます。

》正規分布については、第２回を参照してください。

次に「有意水準」を決めます。平均値のデータの正規分布は、分散が既知の場合、N(μ,σ²/n)で表すことができます。μはサンプリングしたデータの平均値、σはサンプリングデータの標準偏差（※）、nはサンプルサイズ（サンプルの個数）です。

※標準偏差はExcelの関数「STDEV」で算出可能です。データのばらつきを示す指標の1つ。
※分散は関数の「VAR」です（標準偏差の計算で平方根（√）を出す前の値です）

今回の場合、改善前の平均値は10、標準偏差は0.5になり、サンプルサイズは10でした。なので改善前の平均値はN(10,0.5²/10)の正規分布になります（図1）。

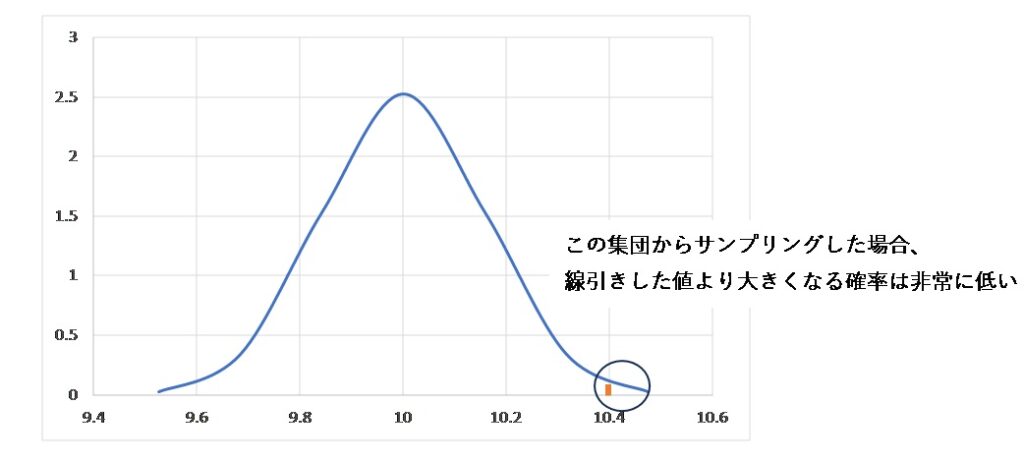
図1の縦軸は、平均値が出現する頻度を表していると考えてください。平均値である10から値が大きくなるほど(また小さくなるほど)、出現する確率はどんどん下がります。

そして、偶然出る値であれば、出現率はかなり高いはずです。逆に、あまりに出現確率が低い平均値が確認されたら、偶然出るのだとしても、そうそう出てこないということです。

だから、後者であれば、改善前からサンプリングしたものではなくて、別の集団（例えば改善された設備)からサンプリングされたもの）といえる、つまり偶然出た差などではなくて、改善前後の差のデータだろうと判断できるのではないでしょうか？

「どの程度低い確率のデータが示されれば、帰無仮説を否定できるのかどうか」の共通基準となる確率を「有意水準」と言います。研究や実験では、一般的に5％で設定することが多いです。

次に検定統計量を決めます。今回扱う正規分布は標準正規分布というものに変形させると、どの値がどのくらいの確率で発生するのかを知ることができます。

そして正規分布を標準正規分布に変形させるためには以下の計算を行います。ここでは「z検定」を用いるので、ｚ値求めます。

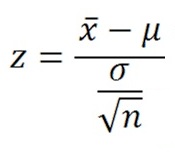
xbar(x̄)は、今回の場合は改善後の硬度の平均値です。そしてこのz値が検定統計量になります。このzが標準正規分布のどの辺に位置するかで、検定を行うわけです。

今回の例でz値を換算すると、

z=(12-10)/(0.5/√10)=12.6

になります。

対して、標準正規分布において有意水準5％となる確率変数（z0）は1.64（※）です。
つまりz値に換算して1.64以下の範囲におさまる硬度となる確率は5％以下ということです。

※正規分布の確率は計算で求めることもできますが、あらかじめ確率がまとめられている表から簡単に探せます。統計関連の教科書（巻末に参考文献）の付録として付いていることが多いです。

今回の改善後の硬度12というのはz値に換算すると12.6になりました。

なので、1.64より明らかに大きいので、改善前と同じ集団（改善前の装置と同様の条件からのデータ）からサンプリングして、偶然出た数値とは言い難いよねとなります。

なので改善前と改善後が等しいという帰無仮説は棄却（否定）され、改善前より改善後の硬度の方が高いという対立仮説が採用され、「改善されたと考えてもいいだろう」という結論が導けるわけです。

以上が検定の基本的な流れですが、かなり端折って説明しており分かりづらい点も多いかと思います。もっとちゃんと知りたいという方は私のチャンネルの解説動画をご覧ください。

で、なんで検定を使っちゃダメなのか

さてここからようやく、本題の検定を使っちゃダメな理由を解説いたします。

主な問題点は以下になります。

1. 「差がないこと」を積極的に言えない
2. 有意水準は本当に5％でいいのか？
3. サンプルサイズで結論が変わる
4. 統計的有意差は技術的な有意差とは異なる

まず、差がないことを積極的に言えません。先ほどの事例で例えば改善後の硬度が小さく、帰無仮説が棄却できなかった場合、「差がない」と断言できないのです。あくまで、「今回は差があるとは言えなかった」という結論になります。つまり、「次回改めて検定したら差が出るかも」とか「サンプルサイズをさらに大きくしたら差が出るかも」という見解が込められているのです。

これは検定を学び始めの人がやりがちな誤りでして、最初に私が学び始めた動機である、「4M変更を実施したけど、変更前と同じ品質であることを言いたい」（つまり、データに差がない）という用途には使えないのです。

有意差検定は、あくまで「データに差があるといってもいい」と言い訳をするための道具です。「データに差がない」ことをそれと同じように説明しようとしても、結局、「データが少なすぎてたまたま差が見つからなかっただけじゃね？」など、分かりようがないからです。

次に有意水準は、本当に5％で良いのでしょうか？

通例的には5％か1％が使われています。しかしこの5％の理由には特に根拠がありません。

R.Aフィッシャーさんが「1/20で起きるならレアっていえるんじゃね？」「5％にしてたら標準正規分布で約2になって使いやすいんじゃね？」などと言ったなどの噂を耳にしますが、実態は不明です。

そもそも5％という値が稀というのは、とりあげる事象によるでしょう。比較対象がないのに単一の値(5％)の出現率が「珍しいこと」と決めつけるのは無理があります。

次にサンプルサイズによって結論が変わります。非常に深刻です。以下の式の分母に注目してほしいのですが、

xbar, μ, σが一定として、大量のサンプルを測定したと仮定します。標準偏差σの分母にnが存在しています。つまりnが大きくなるほど、分母全体が小さくなります。一方分子の値は一定です。よって最終的にz値が大きくなります。サンプルサイズが10から1000になっても普通は平均値も標準偏差も大して変わらないですよね？

でも検定的には差が出やすくなるのです。実態は何も変わっていないのに！　実は検定においては、結論を誤らないために適切なサンプルサイズを算出する手法も存在しています。しかし、このあたりの手法は、通常の検定を扱うよりもっと難しいし、そもそも統計なんてものはデータが増えるほどに精度が増すものなのに、この検定という手法においては“ほどほどにしてね”という統計の常識に反するものになっています。私が検定を信用できなくなった最たる理由がここにあります。

そして3つ目が、検定を用いて判断した有意差が、技術的な有意差とは限らないという点です。例えば、「コンビニのおにぎり100gを101gに増量しました」という話があるとしましょう。これまでは100gのおにぎりを標準偏差0.1gの精度で提供していたので、1gの増量というのはその精度と照らし合わせると統計的には増量したと言えます。しかしながらおにぎりの1gの差を感じ取れる人間がこの世にいるんでしょうか？　明らかにおかしい話を私はしていますが、「検定における有意差を妄信する」ということは、つまり、こういうことなのです。

これはモノサシが違うことによって生じています。検定のモノサシはデータのばらつきです。標準偏差が単位になっているのです。一方製品のモノサシは品質項目によって異なります。おにぎりであれば胃袋の具合によるし、色ならば視覚が違いを感じ取る差分（ΔE>3とか)だったりするでしょう。重さと長さを比較するくらい無茶な話をしているわけです。

そもそも技術的な数値の差というのは、技術のノウハウの根幹です。このくらい値に違いが生まれたら顧客にインパクトを与えるという情報なのですから。そこを技術者自身が見極められず(見極めようとせず)、統計的手法が自動的に答えを返してくれるから依存しようという心根が土台間違っているのです。

……過去の私にも言っています。書いてて泣きたくなってきました・……。

まとめ

このように、有意差検定には問題があります。今回取り上げた平均値の検定だけでなく、正規性の検定、相関性の検定、F検定をもとにした分散分析、全てに問題があるのです。正直サンプルサイズを適切に導きつつ、慎重に扱っていくのは難易度が高いので、そんなに気を使うくらいなら使わらない方がマシだと私は考えています。 結局技術者なら測定した値に差があるかどうかは、顧客の情報を吸い上げ、自らの技術力を高めて判断しなさいということになるのでしょう。

関連リンク：熊野コミチ 統計とお仕事チャンネル（YouTube）

記事一覧：【連載】熊野コミチの「ものづくり統計学」

参考文献
本当にわかりやすいすごく大切なことが書いてあるごく初歩の統計の本　吉田寿夫・著（北大路書房）

---

執筆者プロフィール