正規分布してるかどうかが分かる「Q-Qプロット」って何だ？｜熊野コミチの「ものづくり統計学」【第2回】

そのデータは正規分布か、そうじゃないのか。それが問題だ！

統計学、特にQC手法に使われている手法の多くは正規分布を前提としています。というのもモノづくりというのは、特定の品質を狙ってばらつきが小さくなるように行われます。それでもどうしても狙いの品質に対して前後に値が振れてしまう。なので異常事態がない場合、製品の品質データは正規分布の傾向を取ります。なので正規分布を前提とした手法群は品質管理と相性が良いわけです。

なので重要なのは、今分析しようとしているデータが正規分布であるか否かということです。正規分布でないなら、工程能力指数とか標準偏差をもとにした3σ管理とかは使えないし、そもそも想定外のアクションが入り込んでいるので層別などをして、異常の特定をする必要が出てきます。正規分布か否かでその後のアクションがガラッと変わる。つまり、その見極めが非常に重要なわけです。

さて、では貴方は正規分布かどうかをどうやって見極めていますか？

ヒストグラムですか？

おそらくですが、「ヒストグラム」と答える方が多いかもしれません。実際、私も過去に何かのコンサルからそのように習った記憶があります。ですが、実は推奨できません。というのもヒストグラムで正規分布の見極めは非常に難しいんです。

手元にEｘcelがあったら試してほしいのですが、norm.inv関数、そして確率の部分をrand関数、平均は0、標準偏差は1とします（下記）。

=norm.inv(rand(),0,1)

30個のサンプルを無作為抽出した数を出す

これを30個コピペすると、「標準正規分布から30個ランダムで抜き出したデータ群」が出来上がります。

さらに、それを30個分作ってみてほしいのです。この30個のデータはランダムに標準正規分布から抜き出したデータになります。このデータでヒストグラムを作ってみるとどうでしょう？

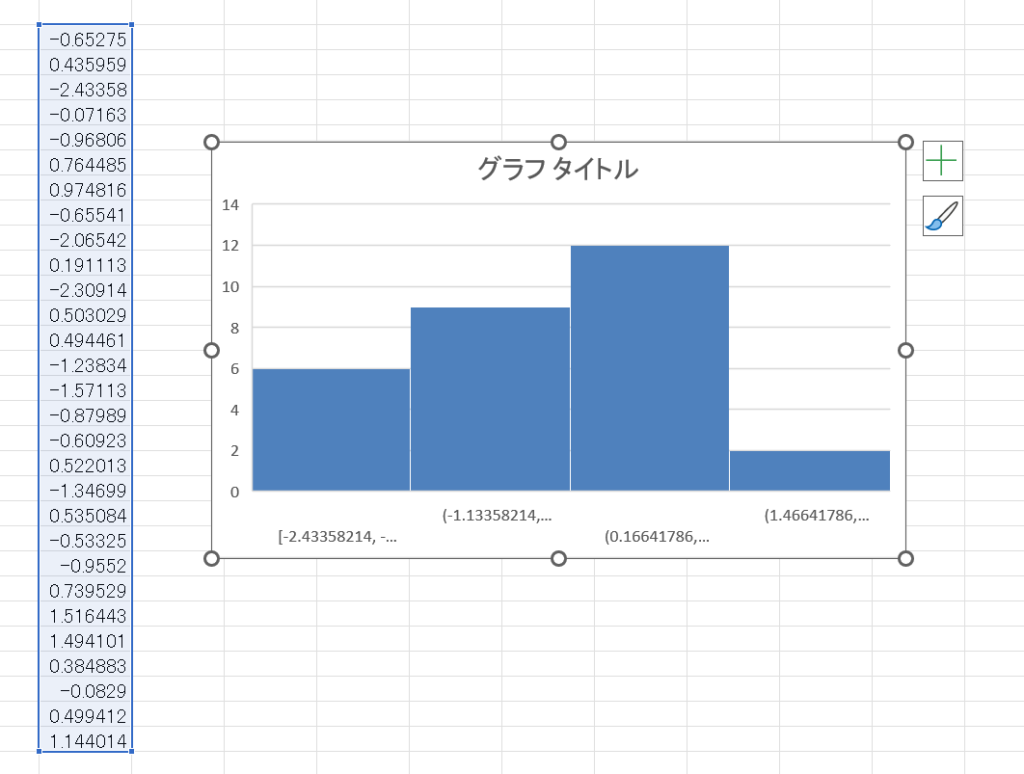
はい正規分布しません。

由来は言うまでもないほど正規分布なのに、正規分布の形にならないのではないでしょうか？少なくとも何回か繰り返すと正規分布にならない回数の方が多いと思います。

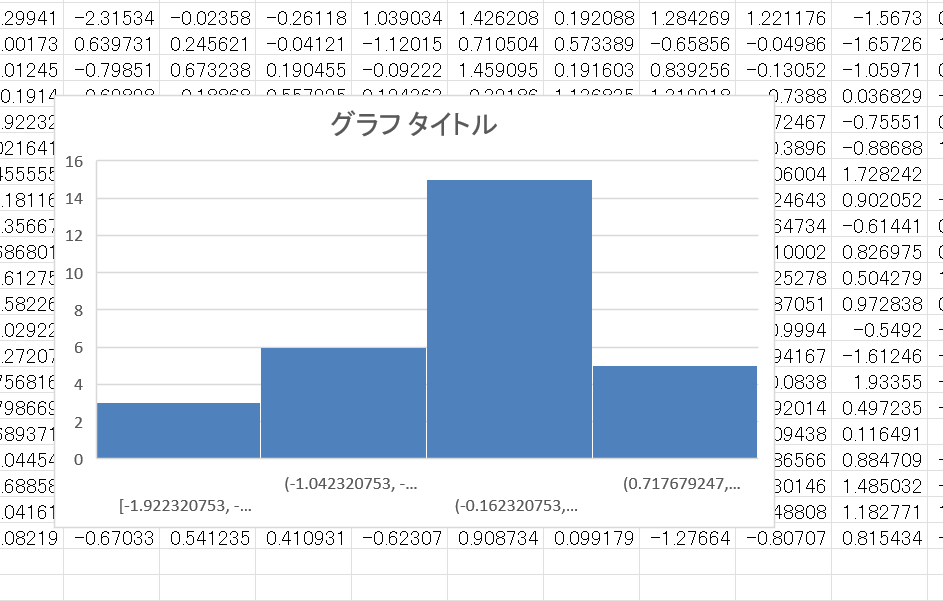
増やしてみたけど、なりません……

このようにヒストグラムでは30個程度のデータでは正規分布かどうかを見極めるのは非常に困難なんです。ちなみに100個でもたまに怪しいです。1000だとずいぶんと安定します。製造業では量産時のデータであれば、1000のデータを取ることも可能かもしれませんが、品質不具合などで波及範囲を絞ったりするとデータ量を確保できない可能性は十分に出てきます。

そうなると統計手法を使っていいのか判断が付かない。大変困ったことになってしまいます。

正規分布かどうかを判断するには、Q-Qプロットだ

そこで便利なのがQ-Qプロットです。この手法を使えば、30個かそれ以下でも正規分布か否か判断することが可能になります。ちなみにデータ多くても同様に判断可能です。覚えておいて損はありません。

基本的なプロセスは、以下の通りです。

• データの順位を付ける
• データの順位からその順位が発生する確率を割り出す。
• データの平均値と標準偏差を算出する。
• ②の確率に対して、③の平均値と標準偏差であればどのようなデータが本来期待されるか算出します。
• 生データと④のデータで散布図を作り、直線関係の度合いを確認します。

とりあえず正規分布から30個データを抜き出してやってみましょう。

ちなみに今回取り上げたデータでヒストグラムを作るとこんな感じです。

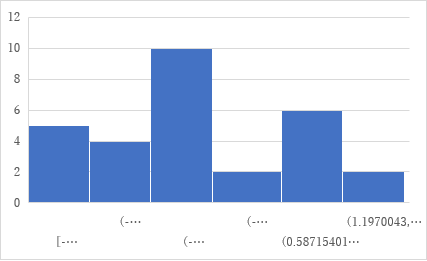
むむ？

お世辞にも正規分布しているとは言えないデータです。

まず順位付けです。エクセルではrank関数を使えば簡単に全データのうち、注目しているデータの順位が容易にわかります。ちなみに順位付けは昇順になるようにしてください。

=rank(生データ、参照元、1) 3番目の値を1にすると昇順になります。

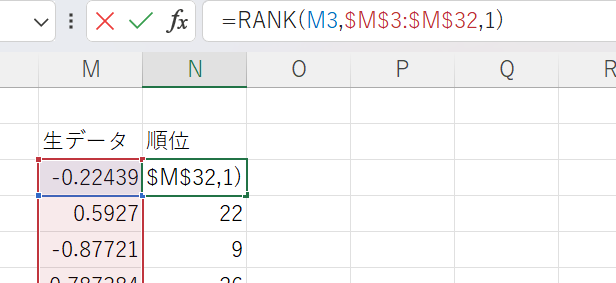
次に順位からその順位が発生する確率を計算します。これには以下の計算式を使います。

=(順位-0.5)/N　Nはサンプルの数です。

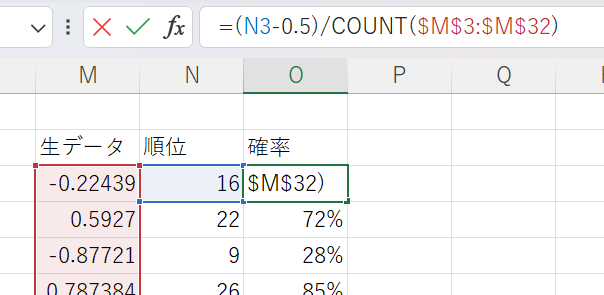
そして生データの平均値と標準偏差を計算します。

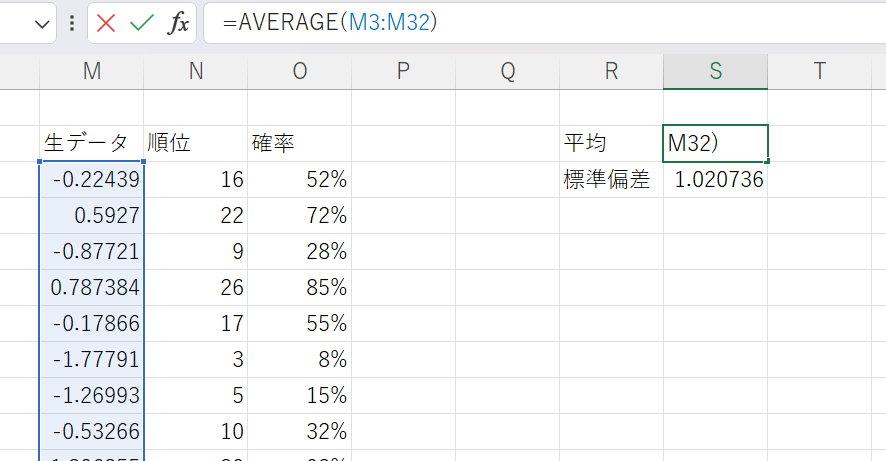
この平均値と標準偏差からは理想的な正規分布が導かれます。その理想的な正規分布とデータの発生確率を照らし合わせると、期待される確率変数が導かれるわけです。

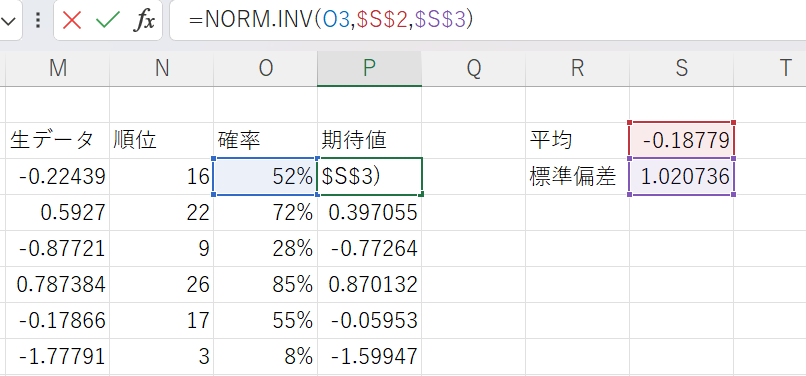
ちなみにnorm.inv(確率、平均値、標準偏差)と打ち込めば期待値は簡単に計算できます。

最後にこの期待値と生データを標準化して散布図を描いたら完成です。

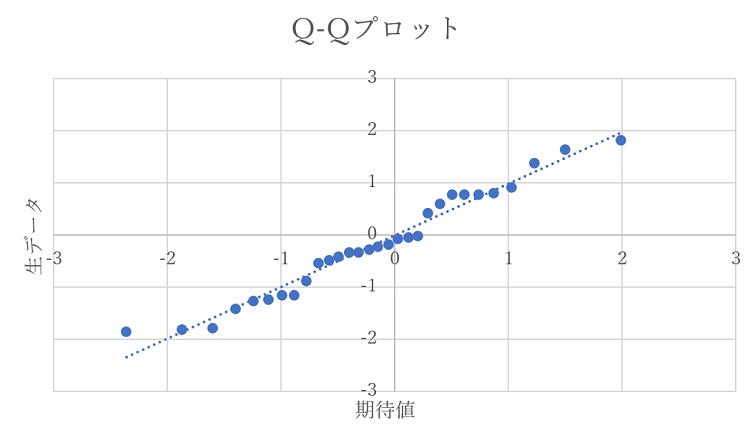
要は正規分布であれば期待できるデータとどれだけ同じようになっているのか、という視点で分析しているわけです。なので直線性が良いほど正規分布であることを意味します。

今回30個のデータで作ったQ-Qプロットはかなりきれいに直線に乗っているので、正規分布であると断定しても良いでしょう。

この手法はQC向けの教科書に載ってなかったりするので、知らない人が案外多いです。また知っていても統計ソフトによる分析が前提とも思われたりしているのですが、今回示したようにExcelでも十分活用可能な手法です。直線性に注目するのでサンプルサイズが30程度でも十分解析可能なのでぜひ使ってほしいです。

「つか、どっからが直線やねん！」――Q-Qプロットの注意点

このように便利なQ-Qプロットですが、注意点もあります。

「どこからが直線性があるって言えんねん！」って話です。かなり視覚的な手法なので、人によって「ここから直線だ」っていうのが異なるんですよね。

実際絶対的な指標が無いのが現状なのですが、チェックするポイントはいくつかあります。

まずはy=xに乗っているかどうかを確認しましょう。Ｅｘｃｅｌの「近似曲線」を使えば線形近似の直線を勝手に引いてくれます。そしてオプションの中の「切片」の設定を0にし、数式の表示を行えばy=axの関数が表示されます。このaの値が1に近いほど正規性(正規分布かどうか)が良いといえます。0.9から1.1の間には入っててほしいです。

次にy=xのモデルに対する相関係数です。いくら傾きが1に近いといっても、その直線状にデータが載っていないと意味がありません。そこで相関係数でy=x上にデータが乗っているかを確認します。こちらは、0.95以上は欲しいところです。

そして最後にQ-Qプロットの端っこに注目。

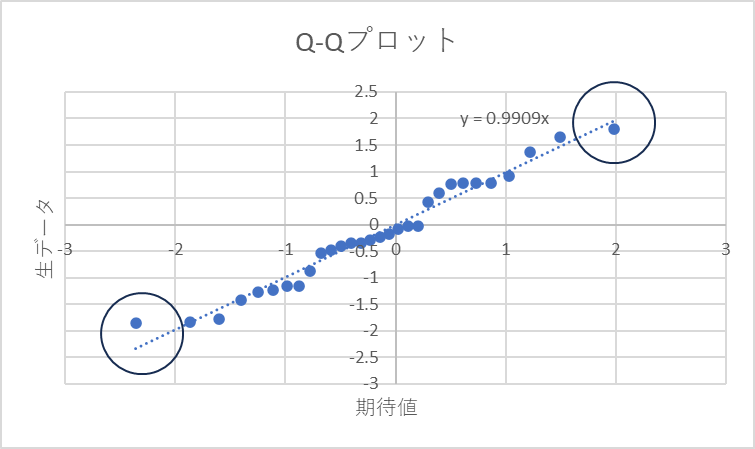
図の〇のあたりです。

ここが極端に直線から外れいてる場合があります。その場合は、正規分布の裾野部分に何かしらの異常が出ていてy=xや相関係数に問題が無くても正規分布として扱えない場合がありますので要注意です。

以上の3点に注目して特に問題がなければ正規分布と判断してもよかろうかと思います。

ただこういう視点を解説しちゃうと、Q-Qプロットを描いても、先ほどのような指標（y=xや相関係数)にばかり目が行ってしまって、せっかくのグラフをおろそかにしてしまうもの。出来れば指標をあまりあてにせず、プロットをちゃんと観察することをお勧めします。

「正規性の検定」はやめておくべし

もう1つ注意点があります。正規性の検定という手法がありますが、検定による正規性の判断はやめた方が良いです。統計ツールにはShapiro-wilk検定をはじめとした様々な正規性の検定手法があります。しかし検定というのは「等しくない」という結果を積極的に返す手法であり、等しいという結果を下すのに向いていません。

そして正規性を問う場面では「正規分布と等しい」という結果が欲しい場合が多いと思いますが、検定という手法の仕組み上、結論として「今回は等しくないとは言えない」という消極的な結論しか導けません。「今度やったら、サンプルサイズを増やしたら結論が変わるかもね」という意味合いを含んでいるんです。そのくせp値が0.05より低いかどうかの二元論で話が進みますから、使う癖が付くとプロットに全く注目せずに判断してしまうという危険を冒しやすくなります。検定の危険性については、次回詳しく解説しますので楽しみにしていてください。 今回はQ-Qプロットを紹介しました。データが少なくても正規性を判断できるツールなので手札として持っていると非常に便利です。直線性という若干判断があいまいな部分があるツールではありますが、その辺は他のグラフも事情は似たようなものですから、実用を繰り返して慣れていってくださいね。

（次回へ続く）

関連リンク：熊野コミチ 統計とお仕事チャンネル（YouTube）

記事一覧：【連載】熊野コミチの「ものづくり統計学」

---

執筆者プロフィール