目次
関連リンク：「図面管理」に関する記事一覧
ベルヌーイの定理の基本概念
ベルヌーイの定理は、18世紀のスイスの物理学者ダニエル・ベルヌーイによって発見された基礎原理です。製造現場では、液体や気体といった流体を扱う場面が数多く存在します。化学プラントの配管、冷却システムの設計、空調設備の最適化など、流体の挙動を正確に予測することが品質管理とコスト削減に直結します。
流体とエネルギーの関係
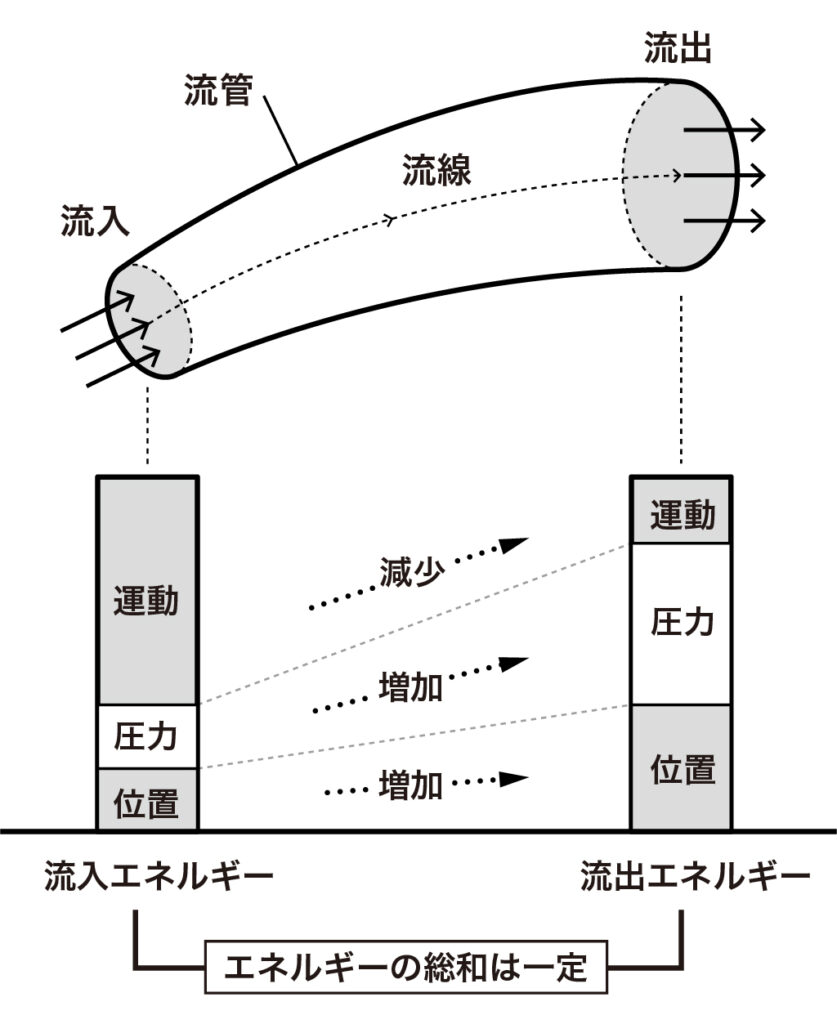
流体が持つエネルギーは、圧力エネルギー、運動エネルギー、位置エネルギーの3つの形態で存在し、これらの合計は流れに沿って一定に保たれます。この原理こそがベルヌーイの定理の本質であり、流体システムの解析における出発点となります。
圧力エネルギーは流体が周囲に及ぼす圧力から生じるエネルギーです。運動エネルギーは流体の速度に由来し、位置エネルギーは流体の高さによって決まります。製造設備の設計では、これら3つのエネルギー形態のバランスを考慮する必要があります。
定理が適用される条件
ベルヌーイの定理を実務で適用する際には、いくつかの前提条件を理解しておく必要があります。これらの条件を満たさない場合、定理の予測精度が低下し、設計上の誤差が生じる可能性があります。
第一に、流れは定常流である必要があります。定常流とは、時間が経過しても流れの状態が変化しない流れを指します。第二に、粘性の影響を無視できることが前提です。実際の流体には粘性がありますが、高レイノルズ数の流れでは粘性の影響が相対的に小さくなります。
製造現場では、これらの条件が完全に満たされることは稀ですが、多くの実用的な状況では十分な精度で適用可能です。条件からの逸脱が大きい場合は、補正係数を導入したり、より高度な流体解析手法を併用したりする必要があります。
ベルヌーイの定理の数式と各項の意味
ベルヌーイの定理は数式で表現することで、定量的な解析が可能になります。この数式を理解することで、製造プロセスにおける流体の挙動を予測し、最適な設備設計を行うことができます。実務での流体計算では、この数式を基に配管径の決定、ポンプの必要動力の算出、圧力損失の評価などを行います。
基本式の構成要素
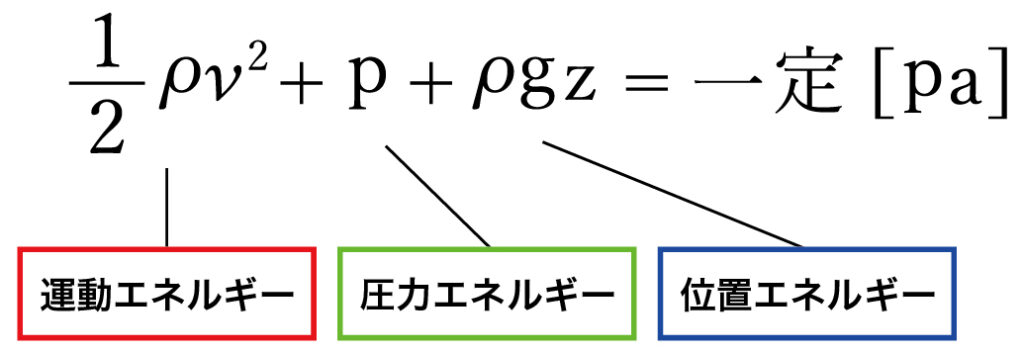
ベルヌーイの定理は「P + (1/2)ρν² + ρgz = 一定」という式で表され、ρは密度、νは流速、Pは圧力、gは重力加速度、zは高さを示します。この式の各項は、それぞれ異なる形態のエネルギーを単位体積あたりで表現しています。
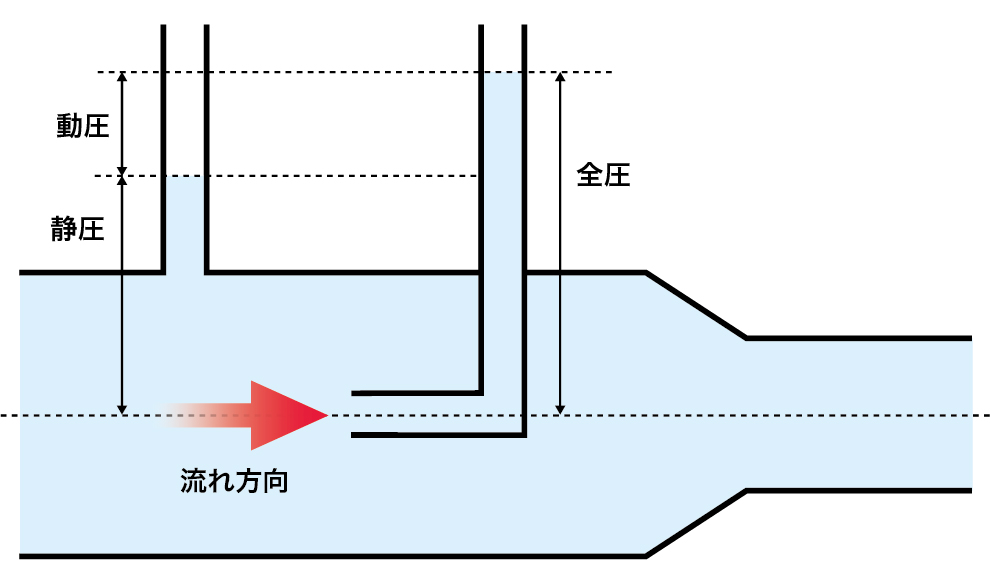
製造設備の設計では、通常これらの項を圧力の次元（Pa）で統一して扱います。各項の単位が揃っていることで、エネルギーの変換や損失を直感的に理解できます。例えば、流速が増加すると動圧が増加し、その分だけ静圧が減少することがこの式から明確に読み取れます。
ρ：密度 [kg/m³]
ν：流速 [m/s]
P：圧力 [Pa]
g：重力加速度 = 9.8m/s²
z：高さ [m]
エネルギー保存則としての解釈
ベルヌーイの定理は、流体のエネルギー保存則の一形態として解釈できます。流体が理想的に流れる場合、エネルギーの総和は流れに沿って保存されるという原理です。
製造プロセスでは、配管の途中で径が変化したり、高低差が生じたりすることが一般的です。このような場合でも、摩擦などのエネルギー損失がなければ、圧力・速度・高さのエネルギー形態が相互に変換されながら総量は保たれます。
実際の製造設備では、配管の摩擦、曲がり、バルブなどによってエネルギー損失が発生します。これらの損失を考慮した修正ベルヌーイの式では、右辺に損失項を追加して実用的な計算を行います。品質管理の観点からは、この損失を最小化することが効率的なプロセス運用につながります。
単位と次元の扱い
ベルヌーイの式を実務で使用する際、単位系の統一が極めて重要です。SI単位系では、圧力はPa（パスカル）、密度はkg/m³、速度はm/s、高さはm、重力加速度は9.8m/s²を使用します。
製造現場では慣習的にkPa、MPa、bar、kgf/cm²など様々な圧力単位が使われることがあります。計算時には必ずSI単位系に統一するか、換算係数を正確に適用する必要があります。単位の取り違えは重大な設計ミスにつながるため、計算過程での単位確認は品質管理の基本です。
- 圧力項（P）：流体の静的な圧力エネルギー、単位はPa
- 動圧項（(1/2)ρv²）：流体の運動による圧力換算値、単位はPa
- 位置圧項（ρgν）：重力による位置エネルギーの圧力換算値、単位はPa
- 全圧：上記3項の合計で、流体の総エネルギーを表現
- 損失項：実際の系では摩擦や乱流による損失を追加
これらの各項を正確に評価することで、配管系全体のエネルギー収支を把握し、ポンプ容量の適正化や圧力制御の最適化が可能になります。
ベルヌーイの定理の原理と物理的意味
数式の背後にある物理的な原理を理解することで、ベルヌーイの定理をより深く実務に活用できます。この原理は、流体粒子の運動を支配する基本法則から導かれており、製造プロセスにおける様々な現象を説明します。
流速と圧力の逆相関関係
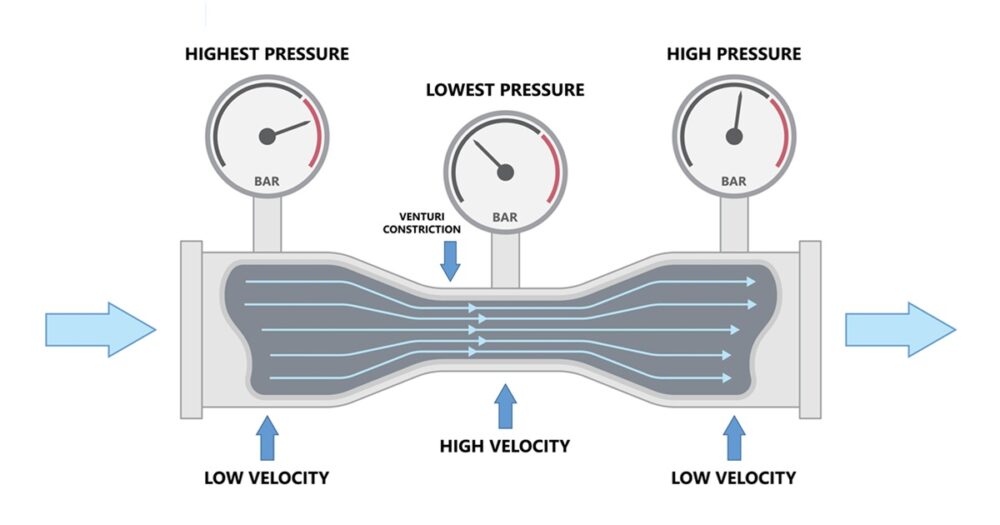
ベルヌーイの定理の最も重要な帰結は、流速が速い場所では圧力が低くなり、流速が遅い場所では圧力が高くなるという関係です。この現象は、エネルギー保存則から必然的に導かれる結果であり、多くの工業的応用の基礎となっています。
配管径が細くなると、連続の式（質量保存則）により流速が増加します。すると、運動エネルギー（動圧）が増加するため、エネルギー保存則によって圧力エネルギー（静圧）が減少します。この原理は、ベンチュリ管や流量計の動作原理として実用化されています。
製造現場では、この関係を利用して流量制御や混合プロセスを設計します。例えば、高速流体の低圧部を利用して他の流体を吸引するエジェクターは、この原理の直接的な応用例です。配管設計においても、縮小部での圧力低下を考慮したシステム設計が求められます。
エネルギー変換の視点
ベルヌーイの定理は、流体のエネルギーが異なる形態間で変換される様子を記述しています。製造設備では、この変換を意図的に制御することで、所望のプロセス条件を実現します。
例えば、タンクから配管へ流体を送る場合、タンク内の高い位置エネルギーが配管内での運動エネルギーに変換されます。また、ポンプで圧力エネルギーを付与した流体は、ノズルから噴出する際に運動エネルギーに変換され高速ジェットとなります。
品質管理の観点では、これらのエネルギー変換過程で損失を最小化し、必要な箇所に必要なエネルギーを効率的に供給することが求められます。配管レイアウトの最適化、適切な機器選定、運転条件の調整などにより、総合的なエネルギー効率を向上させることができます。
製造業におけるベルヌーイの定理の応用例
ベルヌーイの定理は、理論的な興味にとどまらず、製造業の様々な場面で実用的に応用されています。大規模製造施設では、この原理に基づいた設備が多数稼働しており、生産効率と品質に直接貢献しています。以下では、製造現場で実際に遭遇する代表的な応用例を紹介します。配管系統における流量測定
ベンチュリ管やオリフィス流量計は、ベルヌーイの定理を応用した代表的な流量測定装置であり、プロセス制御の要となっています。これらの装置は、配管の断面積を変化させて意図的に圧力差を生じさせ、その差から流量を算出します。
ベンチュリ管は、配管内に滑らかに縮小・拡大する部分を設け、縮小部（喉部）と上流部の圧力差を測定します。連続の式から喉部での流速増加がわかり、ベルヌーイの定理から圧力低下が予測できます。この圧力差は流量の二乗に比例するため、差圧計の読みから流量を算出できます。
製造現場では、化学プラントの原料供給、冷却水の流量管理、圧縮空気の使用量監視など、多岐にわたる用途でこれらの流量計が使用されています。測定精度が高く、可動部がないため保守性に優れており、長期安定運用が可能です。
ポンプとバキュームシステム
ポンプの性能評価や選定において、ベルヌーイの定理は欠かせない理論的基盤です。ポンプは流体にエネルギーを付与する装置であり、このエネルギー付与量を定量的に評価するためにベルヌーイの式が使用されます。
ポンプの全揚程は、吸込側と吐出側のベルヌーイ方程式の差として表現されます。実際の計算では、配管の摩擦損失、曲がりや弁による損失も考慮に入れます。これにより、必要なポンプ性能を正確に算出し、適切な機器を選定できます。
エジェクターやベンチュリスクラバーなどのバキューム装置も、ベルヌーイの原理を応用しています。高速流体の低圧部を利用して気体や粉体を吸引する仕組みは、可動部がなく信頼性が高いため、粉体輸送や集塵システムで広く採用されています。下記のような応用により、製造設備の信頼性向上とコスト削減を同時に実現できます。
- 遠心ポンプの揚程計算：入口と出口の圧力・速度・高さの差から必要動力を算出
- キャビテーション予測：吸込側の圧力低下が蒸気圧以下にならないよう設計
- 配管系のエネルギー損失評価：ベルヌーイ式に損失項を加えて実用計算
- 並列運転時の流量配分：各系統のエネルギー収支から最適配分を決定
- 省エネルギー対策：圧力損失の最小化による運転コスト削減
静圧と動圧の制御
塗装ブースや空調システムでは、静圧と動圧のバランス制御が重要です。ベルヌーイの定理を理解することで、最適な気流分布を設計できます。
塗装ブース内では、均一な気流を作ることで塗装品質を確保します。ダクト設計では、各分岐点での圧力と流速のバランスを計算し、全体で均一な風量分布を実現します。この際、ベルヌーイの定理に基づいて各部の断面積や圧力を決定します。
クリーンルームや無菌室では、室内の圧力を周囲より高く保つことで外部からの汚染を防ぎます。給気と排気のバランス、開口部での気流速度などを、ベルヌーイの原理に基づいて設計することで、一定の清浄度を維持できます。下記の応用例は、ベルヌーイの定理が製造現場で実用的な価値を持つことを示しています。
| 応用分野 | 制御パラメーター | ベルヌーイの定理の役割 |
|---|---|---|
| 流量測定 | 差圧と流量の関係 | 圧力差から流量を算出 |
| ポンプ選定 | 必要揚程の算出 | 系統全体のエネルギー収支評価 |
| 空調システム | 気流分布の均一化 | ダクト各部の圧力・速度設計 |
| 噴射ノズル | 噴射速度と圧力 | 圧力エネルギーから速度を予測 |
まとめ
ベルヌーイの定理は、流体の圧力・速度・高さの関係を表す流体力学の基本原理であり、製造業における配管設計、流量計測、ポンプ選定など幅広い分野で応用されています。この定理は、流体のエネルギー保存則を表現しており、圧力エネルギー、運動エネルギー、位置エネルギーの合計が流れに沿って一定に保たれることを示しています。
製造現場での実務応用では、理論式に加えて連続の式や損失評価を組み合わせることで、実用的な精度で流体系統の解析が可能になります。ただし、定理の適用には非圧縮性、定常流、非粘性などの条件があり、実際の系統ではこれらの条件からの逸脱を考慮した補正が必要です。配管摩擦、乱流、粘性などの影響を適切に評価することで、理論値と実測値の整合性が向上します。
ベルヌーイの定理を正しく理解し適用することで、設備の最適設計、省エネルギー運転、トラブルの未然防止など、製造プロセスの様々な改善が実現できるでしょう。
関連リンク：「図面管理」に関する記事一覧
