ヤング率とは？定義・計算方法と設計での活用ポイントをわかりやすく解説

品質・保全

企画・設計

図面管理

CAD/3DCAD

2025.11.26

製造業における材料選定や製品設計では、材料の機械的特性を正確に把握することが品質と性能を左右します。その中でもヤング率は、材料の変形しにくさを表す最も基本的な指標として、構造設計から品質管理まで幅広い場面で活用されています。しかし、ヤング率の正しい定義や計算方法、実務での活用ポイントについて理解している技術者は少ないのが現状です。本記事では、ヤング率の基礎知識から計算方法、設計現場での具体的な活用方法まで、大企業の製造現場で求められる実践的な知識を解説します。

関連リンク：「図面管理」に関する記事一覧

ヤング率の定義と基本概念

ヤング率は材料の機械的特性を表す最も基本的な物性値の一つです。正式には「縦弾性係数」とも呼ばれ、材料に力を加えたときの応力とひずみの関係から求められます。ここでは、ヤング率の定義と関連する基本概念について解説します。

ヤング率とは何か

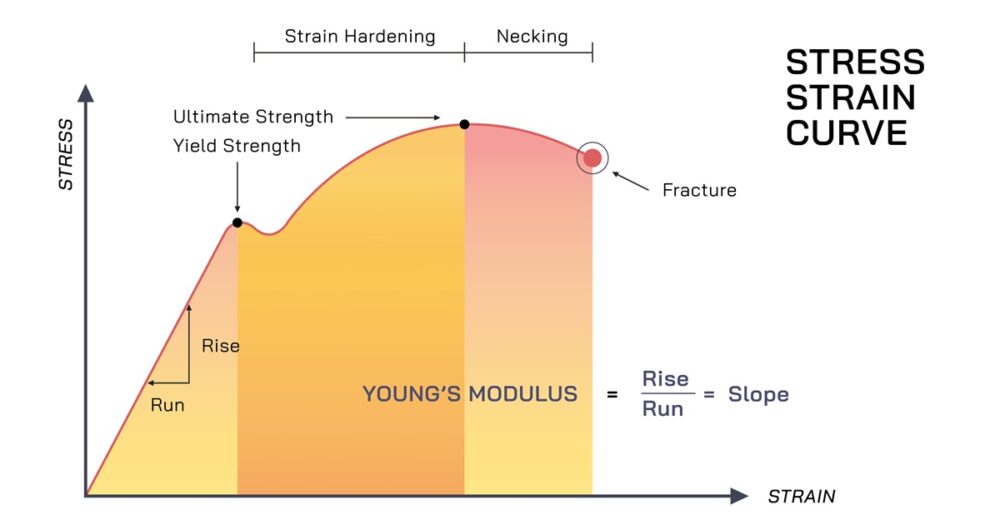
ヤング率は、材料に外力を加えたときの「変形しにくさ（剛性）」を表す物理量であり、単位断面積あたりの力（応力）と変形の割合（ひずみ）の比率として定義されます。この値が大きい材料ほど硬く、同じ力を加えても変形量が小さくなります。ヤング率は材料固有の特性であり、形状や寸法には依存しません。

材料に引張力や圧縮力を加えると、材料は弾性変形します。この弾性変形の範囲内では、力を取り除くと材料は元の形状に戻ります。ヤング率は、この弾性変形の領域における材料の挙動を特徴づける指標として、設計計算や材料選定の基準となります。

応力とひずみの関係

ヤング率を理解するには、応力とひずみの概念を正確に把握する必要があります。応力（stress）は、材料の単位面積あたりに作用する力のことで、単位はPa（パスカル）で表されます。一方、ひずみ（strain）は、材料の元の長さに対する変形量の割合を示す無次元量です。

応力σ（シグマ）は「σ = F / A」で計算され、Fは加えられた力、Aは断面積を表します。ひずみε（イプシロン）は「ε = λ / L」で計算され、 λは変形量、Lは元の長さを示します。弾性変形の範囲では、応力とひずみは比例関係にあり、この関係を表す法則がフックの法則です。

弾性係数との違い

弾性係数は材料の弾性的な性質を表す係数の総称であり、ヤング率はその一種です。弾性係数には、ヤング率のほかに、せん断弾性係数（剛性率）や体積弾性係数などがあります。これらは材料に加わる力の方向や変形の種類によって使い分けられます。

ヤング率は引張や圧縮のような一軸方向の変形に関する弾性係数であり、最も一般的に使用されます。一方、せん断弾性係数は材料をずらすように力を加えたときの変形しにくさを表し、体積弾性係数は材料全体が均等に圧縮されるときの抵抗を示します。設計や解析では、変形の種類に応じて適切な弾性係数を選択することが重要です。下記の比較表も参考にしてみてください。

弾性係数の種類	対象とする変形	記号	主な用途
ヤング率（縦弾性係数）	一軸方向の引張・圧縮	E	構造設計、たわみ計算
せん断弾性係数（剛性率）	せん断変形	G	ねじり設計、せん断応力解析
体積弾性係数	体積変化	K	流体圧力下の変形解析

ヤング率の計算方法と測定手順

ヤング率を実務で活用するには、その計算方法と測定手順を正確に理解する必要があります。ヤング率は理論的な計算式に基づいて求められますが、実際には引張試験などの実験的手法で測定されることが一般的です。ここでは、ヤング率の計算式、単位、そして測定方法について詳しく解説します。

ヤング率の計算式

ヤング率Eは、応力σをひずみεで割った値として定義され、計算式は「E = σ / ε」で表されます。この式から、ヤング率は応力-ひずみ曲線の弾性領域における傾きに相当することがわかります。応力は「σ = F / A」、ひずみは「ε = λ / L」で計算されるため、これらを代入すると「E = (F / A) / (λ / L) = (F × L) / (A × λ)」となります。

この式から、ヤング率を求めるには、加えた力F、試験片の元の長さL、断面積A、そして変形量λの4つの値が必要であることがわかります。実際の測定では、これらの値を精密に計測し、弾性範囲内のデータのみを使用して計算を行います。

ヤング率の単位と表記

ヤング率の単位は、応力の単位と同じPa（パスカル）で表されます。ただし、多くの材料のヤング率は非常に大きな値となるため、実務ではGPa（ギガパスカル、10⁹Pa）やMPa（メガパスカル、10⁶Pa）が使用されることが一般的です。

国際単位系（SI）ではPaが標準単位ですが、分野や地域によっては異なる単位系が使用されることもあります。設計資料や材料データベースを参照する際は、単位の確認と必要に応じた変換が重要です。また、ヤング率は温度や測定条件によって変化するため、測定条件を明記することも必要です。

引張試験による測定方法

ヤング率の測定には引張試験が最も一般的に用いられます。引張試験では、規定の形状に加工した試験片を試験機に取り付け、一定速度で引張力を加えながら、力と変形量を連続的に測定します。このデータから応力-ひずみ曲線を作成し、弾性領域の直線部分の傾きからヤング率を算出します。

測定精度を確保するには、試験片の寸法精度、試験機の校正、変形測定の精度などが重要です。特に変形量の測定には、伸び計（エクステンソメータ）やひずみゲージなどの高精度な測定装置が使用されます。また、試験は通常、常温（23℃±2℃）で実施されますが、使用環境に応じて高温や低温での測定が必要な場合もあります。測定精度を確保するために重要な手順と注意点は、以下のとおりです。

試験片の形状と寸法を規格に従って精密加工する
試験機に試験片を正確に取り付け、軸方向のずれを最小化する
伸び計を試験片の平行部に取り付け、変形量を正確に測定する
一定速度で引張力を加え、応力とひずみのデータを記録する
応力-ひずみ曲線の弾性領域（直線部分）の傾きを計算する
複数回の測定を行い、平均値と標準偏差を算出する

代表的な材料のヤング率と特徴

材料選定においては、各材料のヤング率とその特徴を理解することが不可欠です。ヤング率の大小は材料の用途や設計上の制約に直接影響します。ここでは、製造業で広く使用される代表的な材料のヤング率と、その値が設計にどのような影響を与えるかを解説します。

ヤング率が高い材料の特徴

ヤング率が高い材料は変形しにくく、高い剛性を必要とする構造部材や精密機械部品に適しています。代表的な高ヤング率材料には、鉄鋼材料（約200GPa）、タングステン（約400GPa）、炭化ケイ素（約400GPa）などがあります。これらの材料は、同じ寸法であれば変形量が小さいため、たわみを抑えたい用途に適しています。

高ヤング率材料を使用する利点は、部材の剛性を確保しながら軽量化や小型化が可能になることです。ただし、ヤング率が高い材料は一般的に加工が難しく、コストも高くなる傾向があります。また、高剛性であることは必ずしも高強度を意味しないため、強度と剛性の両面から材料を評価することが重要です。

ヤング率が低い材料の特徴

ヤング率が低い材料は柔軟性があり、衝撃吸収や振動減衰が必要な用途に適しています。代表的な低ヤング率材料には、ゴム（約0.01～0.1GPa）、樹脂材料（約1～5GPa）、アルミニウム合金（約70GPa）などがあります。これらは変形しやすい反面、エネルギー吸収能力に優れています。

低ヤング率材料の利点は、軽量で加工性に優れ、振動や衝撃を緩和できることです。電子機器の筐体や自動車部品など、軽量化と機能性を両立させたい用途で多用されます。ただし、剛性が低いため、荷重を支える構造部材としては不向きであり、用途に応じた適切な材料選定が求められます。

複合材料のヤング率

複合材料は、異なる特性を持つ複数の材料を組み合わせることで、単一材料では得られない性能を実現します。複合材料のヤング率は、構成材料のヤング率と体積分率から理論的に推定できます。代表的な理論モデルには、Voigtモデル（等ひずみモデル）とReussモデル（等応力モデル）があります。

実際の複合材料のヤング率は、これら2つのモデルの中間値となることが多く、繊維の配向や界面特性によって変動します。さまざまな材料におけるヤング率と、その代表的な用途を比較したものです。

材料分類	代表材料	ヤング率（GPa）	主な用途
金属材料	鉄鋼	約200	構造部材、機械部品
金属材料	アルミニウム合金	約70	航空機、自動車部品
セラミックス	炭化ケイ素	約400	切削工具、耐熱部品
樹脂材料	ポリカーボネート	約2～3	電子機器筐体、光学部品
複合材料	CFRP（炭素繊維強化樹脂）	約100～200	航空宇宙、スポーツ用品

設計・材料選定でのヤング率の活用方法

ヤング率は設計計算や材料選定において中心的な役割を果たします。構造強度の確保、たわみの予測、振動特性の評価など、多岐にわたる工学的判断の基礎となる指標です。ここでは、実際の設計現場でヤング率をどのように活用するか、具体的な方法と注意点を解説します。

たわみ計算と構造設計

ヤング率は、梁や板などの構造部材が荷重を受けたときのたわみ量を計算する際に不可欠なパラメータです。梁のたわみδは、荷重、スパン、断面二次モーメント、そしてヤング率によって決まります。片持ち梁の先端にかかる集中荷重Pによるたわみは「δ = (P × L³) / (3 × E × I)」で計算されます。ここで、Lは梁の長さ、Eはヤング率、Iは断面二次モーメントです。

この式から、ヤング率が大きい材料を使用するほど、同じ荷重条件下でのたわみは小さくなることがわかります。精密機械や計測装置など、寸法精度が重要な製品では、たわみを許容範囲内に抑えるために高ヤング率材料を選定することが一般的です。一方、コストや重量の制約がある場合は、断面設計の最適化とヤング率のバランスを考慮した材料選定が求められます。

応力解析と強度評価

ヤング率は有限要素法（FEM）などの応力解析において、材料特性を定義する基本的な入力パラメータです。解析モデルにヤング率を正確に設定することで、部材の変形や応力分布を精度よく予測できます。特に複雑な形状や荷重条件下では、解析による事前評価が設計の信頼性を高めます。

ただし、ヤング率はあくまで弾性範囲内での特性であり、材料が降伏点を超えて塑性変形する領域では適用できません。強度評価では、ヤング率だけでなく、降伏応力、引張強度、破断伸びなどの他の機械的特性も総合的に考慮する必要があります。また、温度や繰り返し荷重などの使用条件がヤング率に与える影響も考慮することが重要です。

振動・固有振動数の予測

機械や構造物の固有振動数は、質量、剛性、そして境界条件によって決まります。ヤング率は剛性を左右する主要因子であり、固有振動数の予測に直接影響します。

振動による共振を避ける設計では、使用環境の加振周波数と固有振動数を離すことが必要です。ヤング率の異なる材料を選定することで、固有振動数を調整し、共振回避や振動減衰特性の改善を図ることができます。回転機械や高速搬送装置など、動的な負荷がかかる製品では、ヤング率を考慮した振動設計が不可欠です。ヤング率を用いた振動設計の主なポイントは、以下のとおりです。