目次
第3回では「作り過ぎのムダ」(筆者がとても嫌いなムダ)について解説しました。作り過ぎたものは「在庫」になります。今回は、「在庫のムダ」にアプローチしていきましょう。
記事一覧:【連載】関伸一の「ものづくりDX研究所」

基本はJust In Time
トヨタ生産方式(TPS:TOYOTA Production System)の2つの基本思想の1つ、「JIT(Just In Time)」を実現すればムダな在庫は生まれません。第3回で、「TOYOTAは在庫を持たないけれど、それはサプライヤーに持たせているだけ。TOYOTAばかり得をして、サプライヤーが損をするのだ」という批判のお話をしました。そしてサプライヤーがJITに対抗するには、自身もJITを実現すればよいとも言いました。
「適正在庫」という考え方があります。読んで字のごとくで、「正しく在庫をする」ということです。在庫の持ち方を「買い方=発注法」で考えてみましょう。発注法には「発注量」と「発注タイミング」の組み合わせで4つの方法があります。(図1)
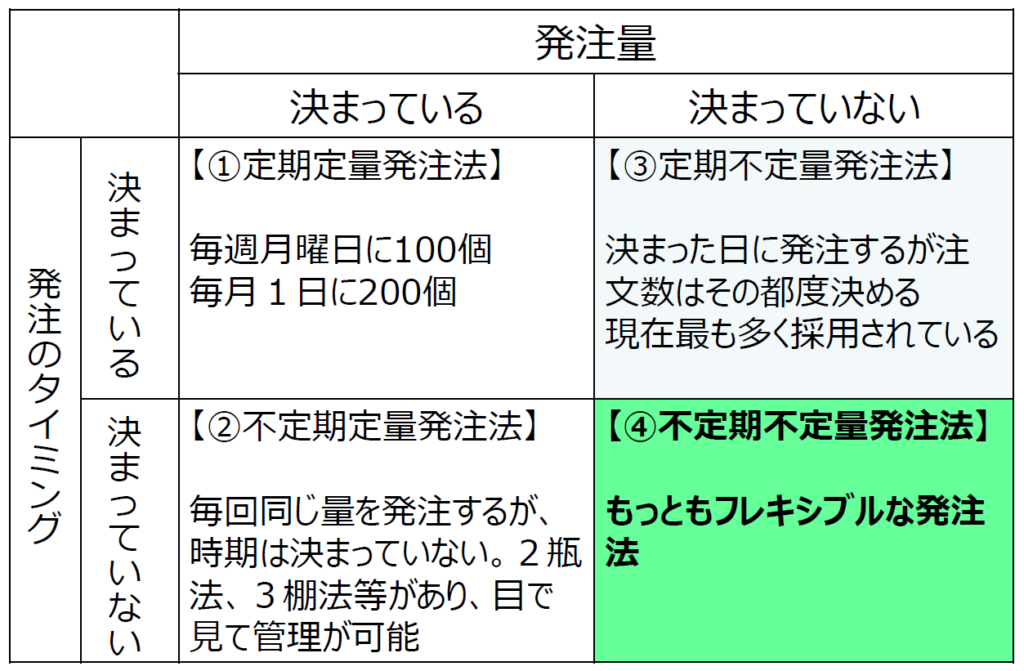
図1①の「定期定量発注法」は決まった日に決まった数量を発注する方法です。筆者の家で定期購入している某乳酸菌入り飲料は毎週火曜日に7本が届きます。これが「定期定量発注法」になり、昨今ではサプリメントなどの定期購入などで一般家庭には普及しているものの、ものづくり企業でこの方法を使っていることはほぼないと思います。
図1②が「不定期定量発注法」で、毎回同じ量を発注しますが、時期は決まっていないという買い方です。例えば自動車整備工場でエンジンオイルを180L缶で2本在庫として持ち、1本が空になったら1本注文するという方法で、目で見てすぐに分かりますし、管理も簡単なので、ものづくり企業では油脂類や大量に使うボルト類などの消耗品で多く使われています。
ただ、中身を見えるようにしておかないと減っていくスピードが見えないため、次の納品がされるまでに在庫を全部使い切ってしまうというリスクがあります。さらに単位の量があまりに多すぎると1本使い切るのに何年もかかってしまい、在庫物が劣化するというリスクもあります。例えば筆者がモーターサイクル整備用にエンジンオイルを180L缶で買ったら使い切るのに10年以上かかってしまいます。だから、せいぜい4L缶を2個ですよね?
図1③の「定期不定量発注法」は、「発注日は決まっているものの、注文数はその都度決める方法」で、現在最も多く採用されています。ですが、「決まった日に納品が集中してしまう」などのデメリットが生じます。また、昨今は物流にまつわるさまざまな問題も多いため、その面でも改善が必要でしょう。
そして最もフレキシブルなのが④の「不定期不定量発注法」です。「いつ、いくつ発注するか分からない」。いわば「Just In Time発注法」です。では、発注時期と発注数をどうやって決めるのでしょうか? そこには平均やバラツキといった統計的手法が必要となってきます。
不定期不定量発注法の考え方
「不定期不定量発注法」は、簡単に言うと過去の使用・発注実績を基に、在庫切れすることも過剰在庫することもない最も合理的な発注法です。手順とその具体例をチャート化したのが図2です。
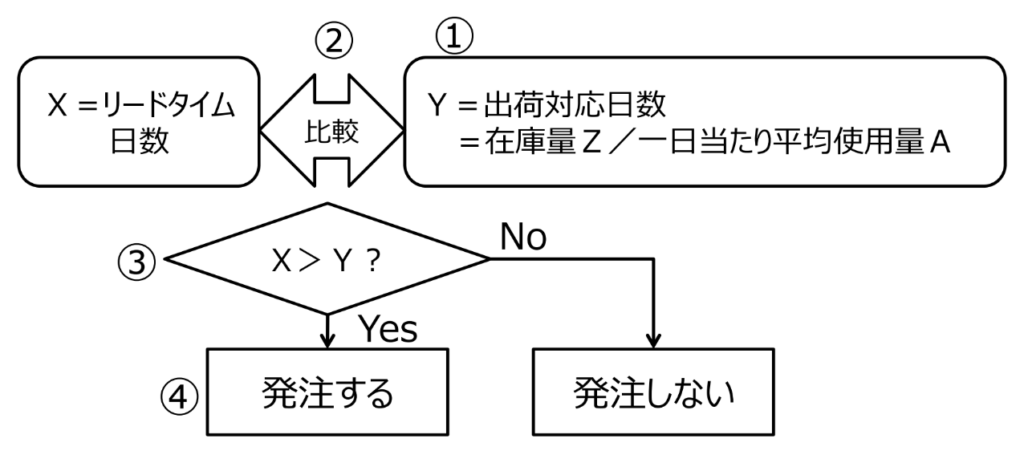
①現在の使用状況の把握:例えば直近10回の平均使用数(A)を求める
②現在の在庫量を評価する:現在の在庫量(Z)が何日分あるか(Y=Z/A)を求める
③発注タイミングを決める:リードタイム(X:発注してから納入までの日数)とYを比較し、X<Yなら発注せず、X>Yなら発注する
④発注数量を決める:最大在庫日数を定め、その分を発注する
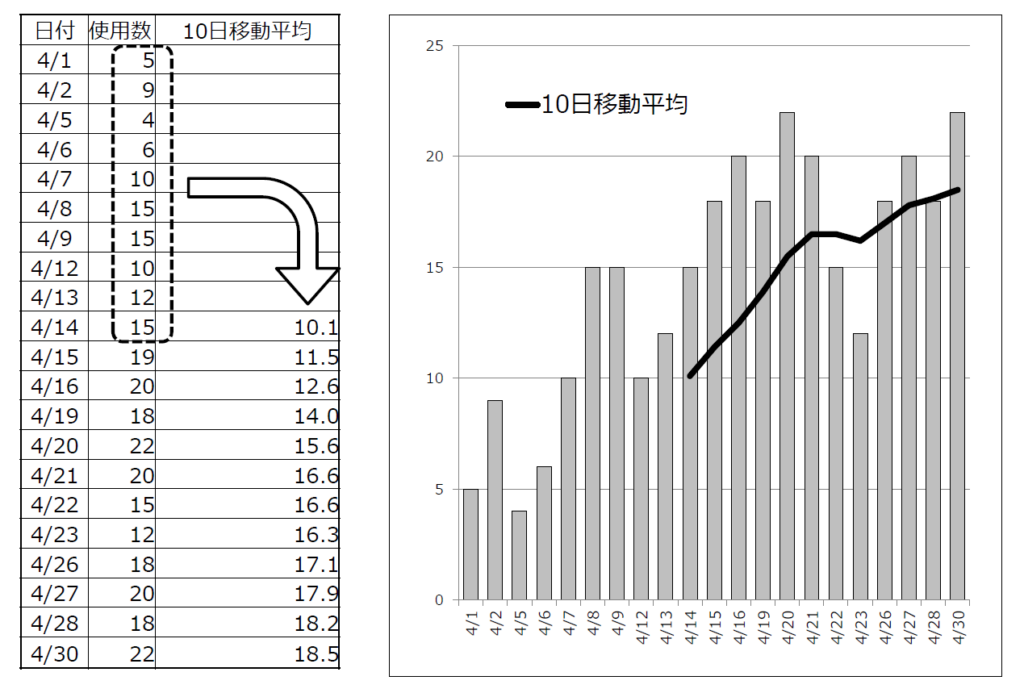
実際の数字を使って分かりやすく解説していきます。図3は、ある部品の4月1~30日の使用数と10日間の移動平均を表とグラフにしたものです。
移動平均は上昇や下降トレンドを判断するのにとても便利で、筆者は愛車の燃費を表計算ソフトに入力し、給油5回分の移動平均をグラフに表示するようにしています。燃費が悪化傾向になれば何らかの不具合(例えば点火プラグ、エアクリーナーエレメントの交換時期など)があると考えて、チェックするためです。
図3で4月14日末時点での在庫は41個です。リードタイム(以下LT)が「2日」、最大在庫日数を「LT+3日」という前提条件で発注タイミングと発注量を計算してみましょう。
〇4月14日:在庫数÷10日間平均使用量=41/10.1=4.1となり、LTの2日より多いので発注は」不要です。
〇4月15日:19個使用したため在庫数は41-19=22、平均使用量は11.5なので22/11.5=1.9となりLTを下回ったため、平均使用量の3日分11.5×3≒35個を発注します。
この発注法を簡易的なグラフにすると図4のようになりますが、実はこれでは在庫切れが頻繁(約50%の確率)に起きます。なぜなら平均値のみを用いて計算していて、バラツキを加味していないからです。
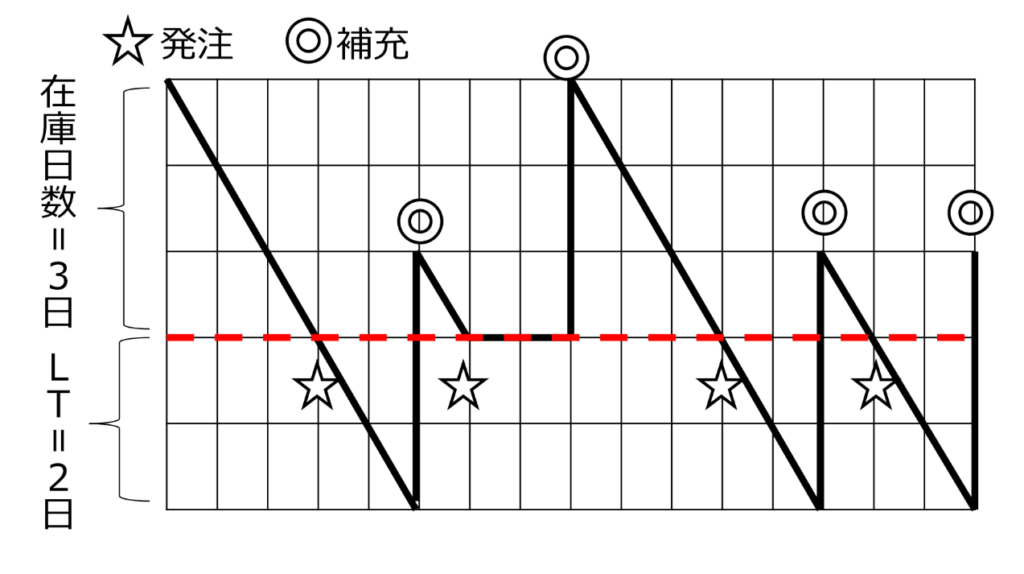
少し乱暴なのですが、使用数が正規分布すると考えると、「平均より多く使用する確率」が50%になるのです。正規分布についてはこのコラムで機会があれば分かりやすく解説したいと思っていますが、筆者は「正規分布を知らなければ正しいものづくりはできない」と断言しているほど重要なものです。「正規分布という言葉など聞いたこともないよ」という読者の方は取りあえずネット検索をしてみてください。
「正規分布」とは
データが平均付近になるほど多くデータが集積する分布。グラフ化すると釣り鐘状の線形になる。人の身長や知能、テストの点数など、世の中のありとあらゆる事象における差は正規分布に従うとされる。工業製品の誤差(ばらつき)もそれに従うという前提で計算するのが品詞管理手法の「シックスシグマ」だ。
在庫切れを防止するために登場するのが「安全在庫」という考え方です。使用数のバラツキによる在庫切れを防止するために適正な数の在庫を持つのです。安全在庫の求め方を表1の上段に記しました。
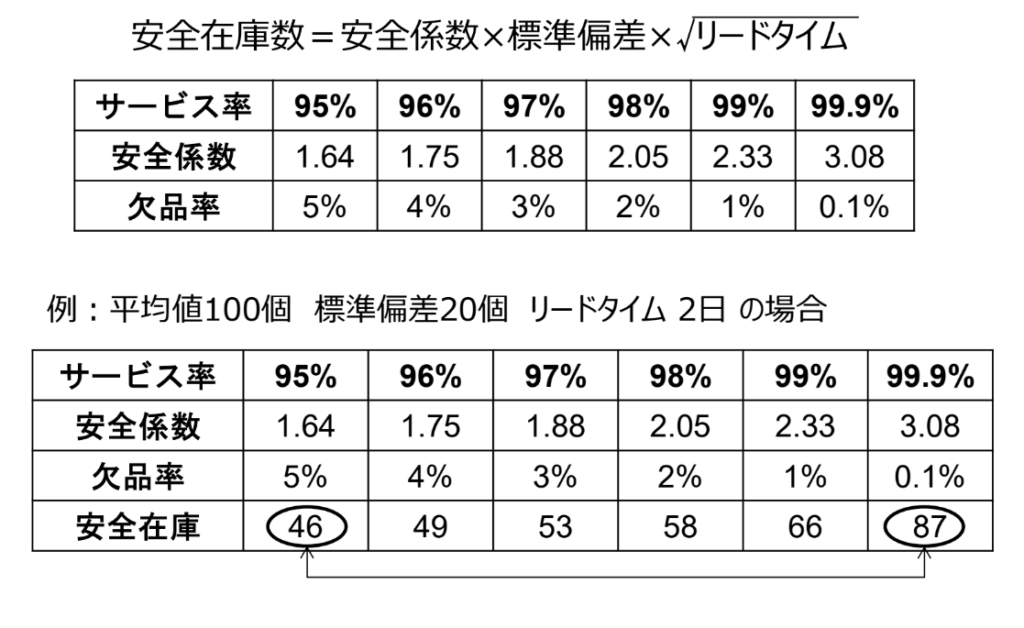
サービス率95%というのは在庫切れの可能性(欠品率)が5%ということを意味し、サービス率を定めれば安全係数が決まります。「標準偏差」(「σ(シグマ)」ともいう)は「バラツキの大きさ」を表す数字で、平均値を求めるのに使用したデータから簡単に求められますが、数字が大きくなるほどバラツキが大きいということになります。この式を使って安全在庫数を求めることができるのです。標準偏差も、ものづくりには欠かせない考え方なので、またあらためて解説できれば良いなと考えています。
例として、平均使用数100個、標準偏差20個、リードタイム2日で安全在庫数を求めたのが表1の下段です。サービス率が大きな数字になれば安全在庫数が当然増えます。この例の場合ですとサービス率95%で安全在庫数が46個、99.9%で87個となります。単価の安いものであれば安全率を高めてもさほど問題はありませんが、単価数百万円の製品や購入備品在庫であったら、安全率と在庫金額のバランスを考慮しなければ資金繰りにも影響を及ぼすことは言うまでもありません。
「いや、在庫切れなど決して起こしてはいけないからサービス率は100%だ!」という場合は、安全在庫を無限大にしなければなりませんよ!
安全在庫の考え方を利用して図4と同じケースでグラフにすると図5のようになり、安全在庫を持たなければ14日目に在庫切れになっていることが分かります。
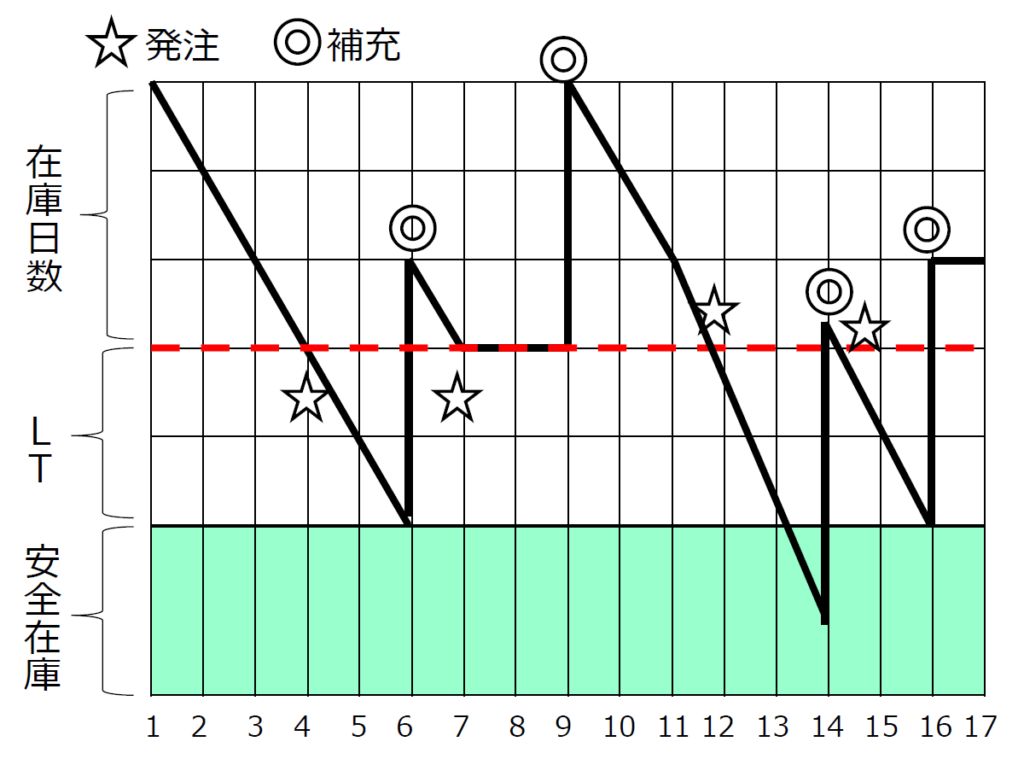
また、安全在庫を求める計算式にLTが入っていることに着目しなければなりません。つまりLTを縮めれば安全在庫数が減ります。極端に言えばLT=0にすれば安全在庫は不要なのです。筆者は「LT短縮」がものづくり企業の競争力強化のための大きな要素だと考えています。LT=0はJust In Timeの概念にぴったり合致するのです。
次回は、デジタル技術を利用した見事な在庫管理システムを紹介いたしましょう。(次回に続く)
記事一覧:【連載】関伸一の「ものづくりDX研究所」
執筆者プロフィール
関 伸一(せき・しんいち)
関ものづくり研究所代表。株式会社Fiot代表取締役。株式会社エコム社外取締役、株式会社桜井製作所社外取締役、国立静岡大学大学院客員教授。
ローランド ディー. ジーにて製造部長として勤務していた時代には、完全一人完結セル生産「デジタル屋台生産システム」を開発。その成果が新聞・雑誌やテレビ番組などで報道されて話題に。ミスミグループ本社では、製造子会社の駿河精機 本社工場長、生産改革室長、環境・品質推進室長を兼務し、業務改善を推進した。
自身の専門である機械工学および統計学を基盤として、品質向上を切り口に現場の改善を中心とした業務に携わる。ISO9001/14001マネジメントシステムにも精通し、経営に寄与するマネジメントシステムの構築に精力的に取り組み、その延長線上として労働安全衛生を含むリスクマネジメントシステムの構築にもかかわる。




