目次
製造業での品質管理を中心としたいろいろな業務の問題解決で使える「製造業新QC/QC7つ道具」について基本から解説します。いまさら聞けない人や、誰かに教えないといけない人も、ぜひご活用ください。
(執筆:小林由美 / facetライター、編集者)
記事一覧:【連載】「新QC&QC7つ道具」基本のキ
関連リンク:「品質管理」に関する記事一覧

マトリックス図法とは
マトリックス図法は、目的や課題に対する手段や性質(期待できる効果、費用、効果が出るまでの時間など)といった要素をマトリックス図にまとめて、それぞれの要素間の関連度や評価について数字や記号などで明確にすることで、問題解決を効果的に進めていく手法です。
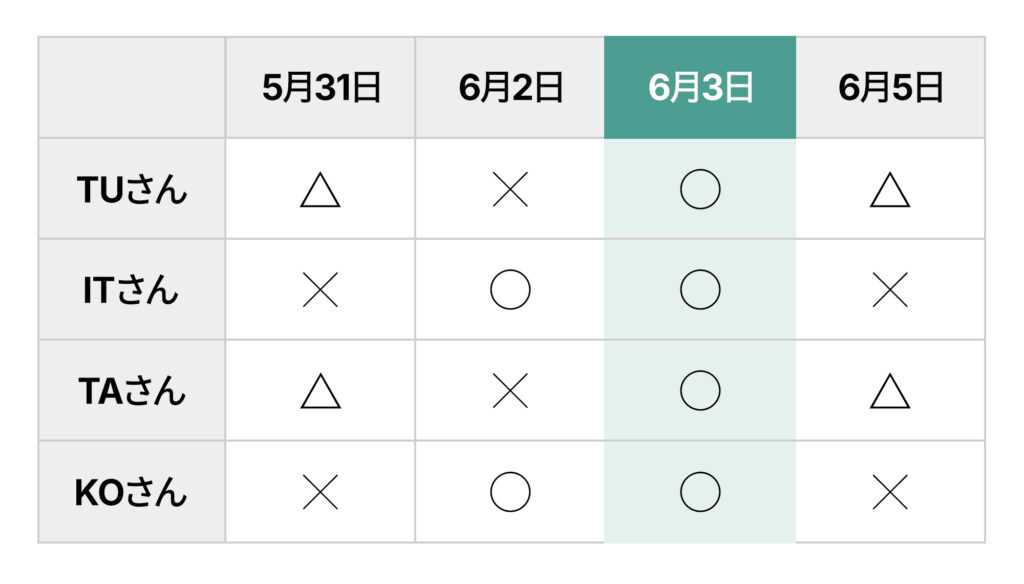
図1はマトリックス図による予定調整の例で、予定の参加者を行に置き、予定の候補日を列に置いています。その日に予定に参加できそうかどうか、○(大丈夫)、△(可能であれば避けたい)、×(不可)といった記号で表現しています。こうした予定調整では関係者が多くなるほど、それぞれの人に次々と予定を聞いていくと混乱しやすいものです。図1からは、6月3日が皆の予定が合うことが一目で分かります。
ミーシーとマトリックス
エンジニアリングの現場で、マトリックス図と共によく使われる言葉が、「MECE(「ミーシー」または「ミッシー」)」です。ロジカルシンキング用語で「ダブりなく、漏れがなく」という意味です。課題やタスクを升目状にまとめて見渡しながらしらみつぶしにチェックしていくマトリックス図は、MECEのために有効なフレームワークの1つでもあります。
なお「マトリックス(Matrix)」は、「母岩・基盤」という意味であり、数学では「行列」の意味で使われます。「長方形状かつ格子状」という行列のイメージを元にした表現です。
マトリックス図の種類
マトリックス図は、主に以下の3タイプがあります。
L型

L型(図2)は、2つの要素を分析する場合に使用する最も基本的なマトリックス図です。図1で示したマトリックス図もL型です。一方の要素を縦軸に、もう一方を横軸に配置します。
T型
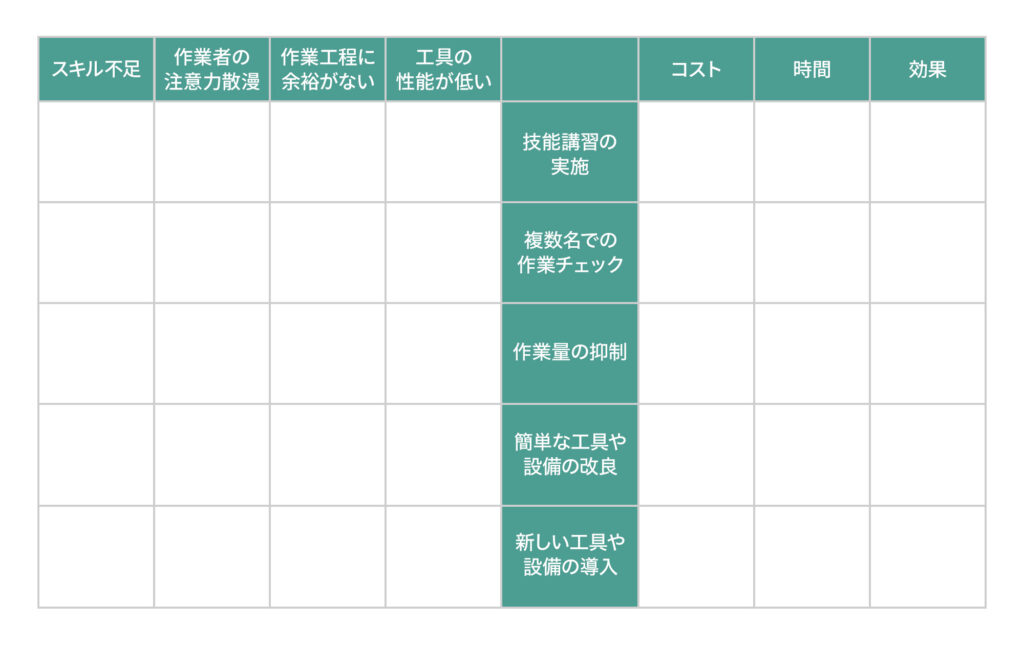
T型(図3)は3つの要素を分析する場合に使用します。全ての要素の組み合わせを考慮するのではなく、A×B、A×Cのように1つの要素に対して残り2つの要素との組み合わせを評価します。そのため形はL型のマトリックス図を組み合わせたような形になります。
X型
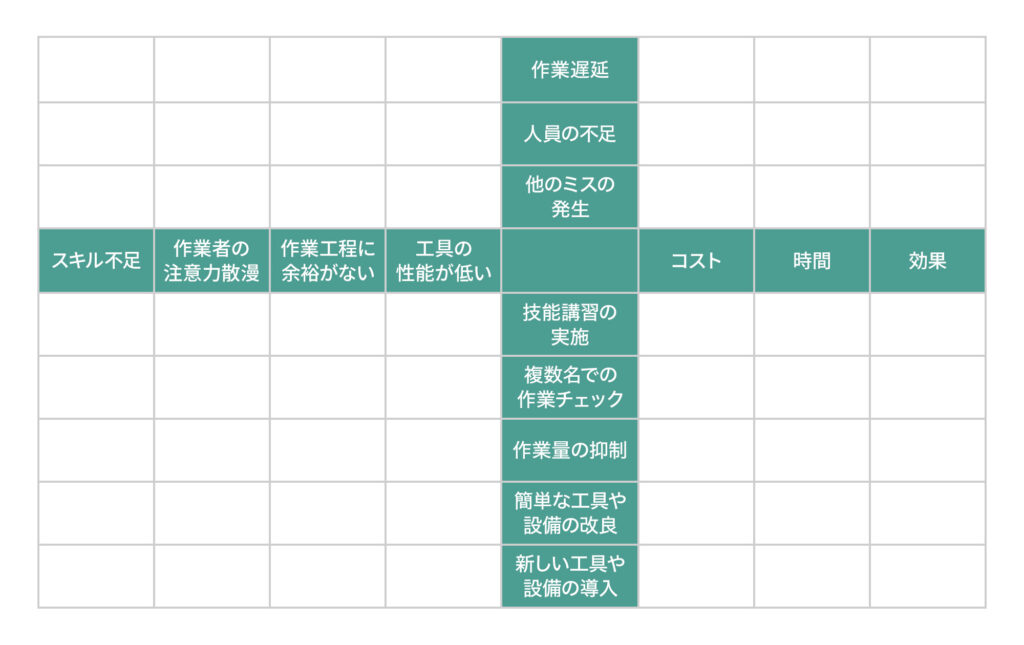
X型(図4)は4つの要素を分析する場合に使用します。L型を4つ組み合わせたような形になっています。
他に、Y型(3次元マトリックス)がありますが、Excelなど帳票ツールでの作図が困難であり、品質管理の現場では用いられることはほぼないことから、ここでは割愛します。
産業用ロボット導入検討でマトリックス図法を活用する
マトリックス図法は、系統図で導いた手段を評価する際にもよく使用します。今回は、系統図にまとめた製造工程をデジタル化するための手段について、マトリックス図法を用いて確認していきます。
部品メーカーのプロトリュード社は、ロボットを導入することで、現場の作業を効率化して、利益率を高めていきたいと考えています。C部品の製造について、面倒な手作業が多いA工程がボトルネックになっていることが明らかになったので、そこを自動化しようと検討しています。このA工程は、Bさんという熟練技術者が担当しています。
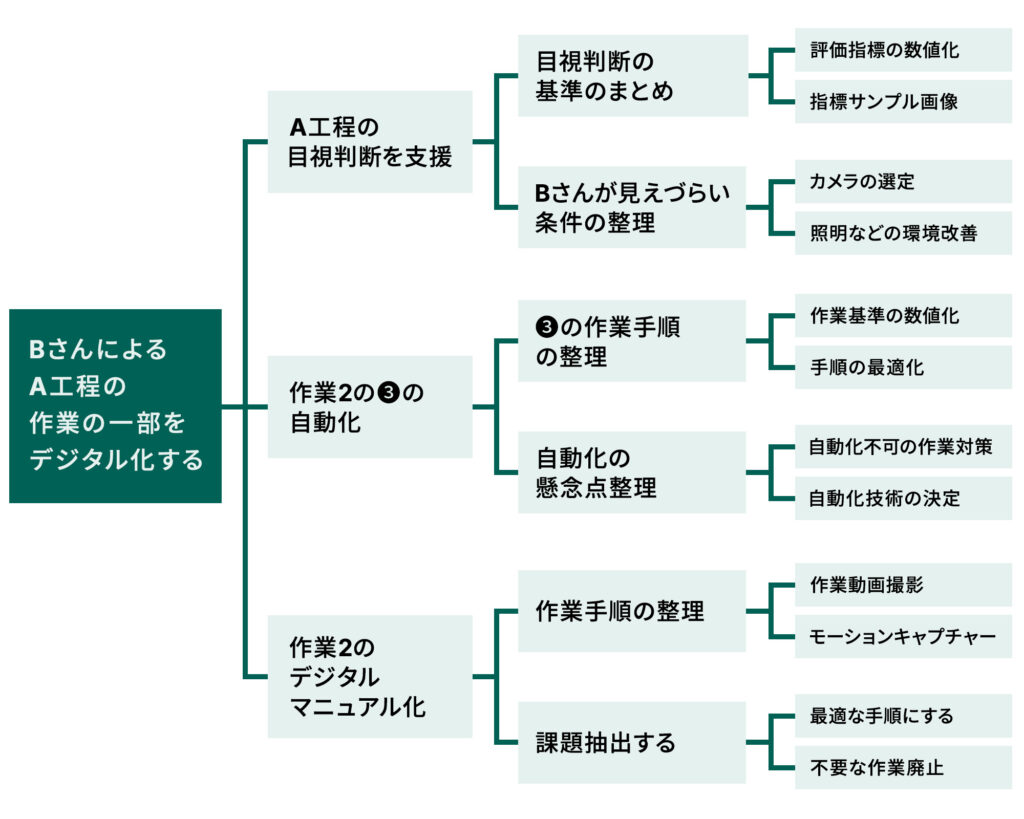
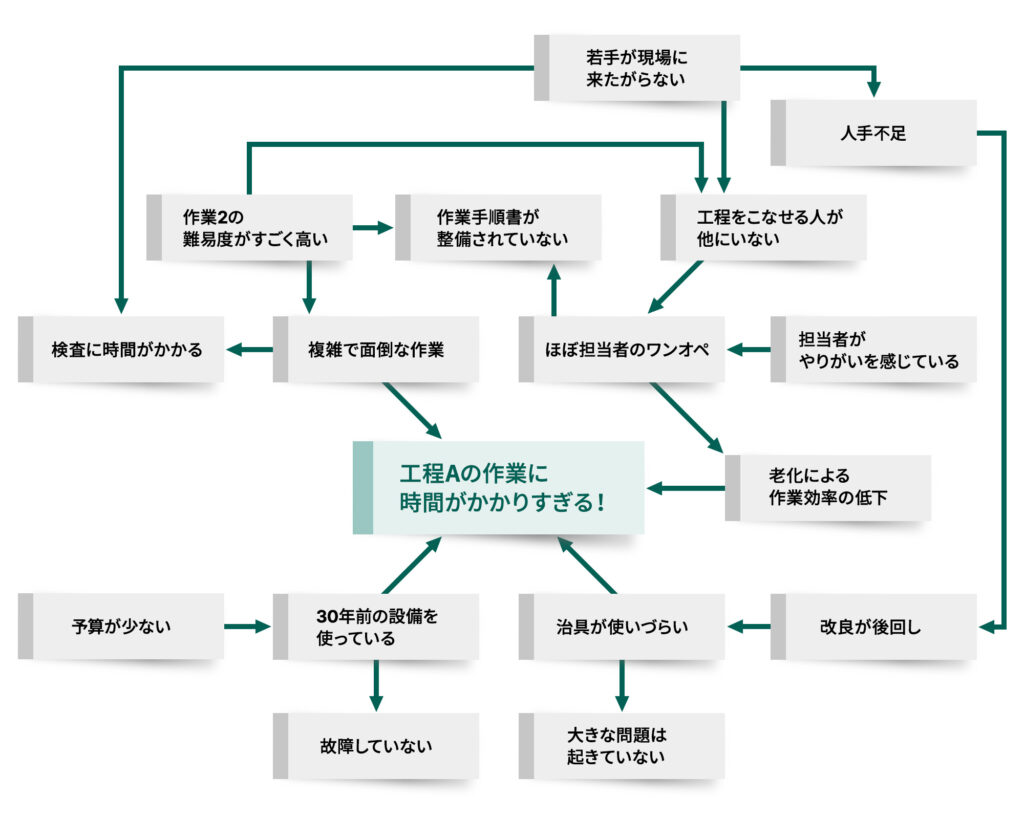
上記の系統図の右端で挙がっている具体的手段について、原因を振り返りながら、マトリックス図法を使って検討します。
関連リンク:【図解】系統図法とは?書き方と読み方も詳しく解説
まず、系統図の手段を一覧で書き出します。

関連リンク:【図解】連関図法とは?書き方と読み方も詳しく解説
系統図を検討した時に参照していた連関図(図7)から、末端の要因と考えていた「予算が少ない」「担当者(Bさん)がやりがいを感じている」「若手に不人気」ということを「原因」として左側に書き出します。図6で書き出した項目は「対策」とします。さらに右側には、難易度と工数を記載します(図8)。
左側には、該当する項目に〇をしていきます。右側の「難易度」にはA~Bで評価を記入します(Aが高い)。想定工数は人月としてみました。
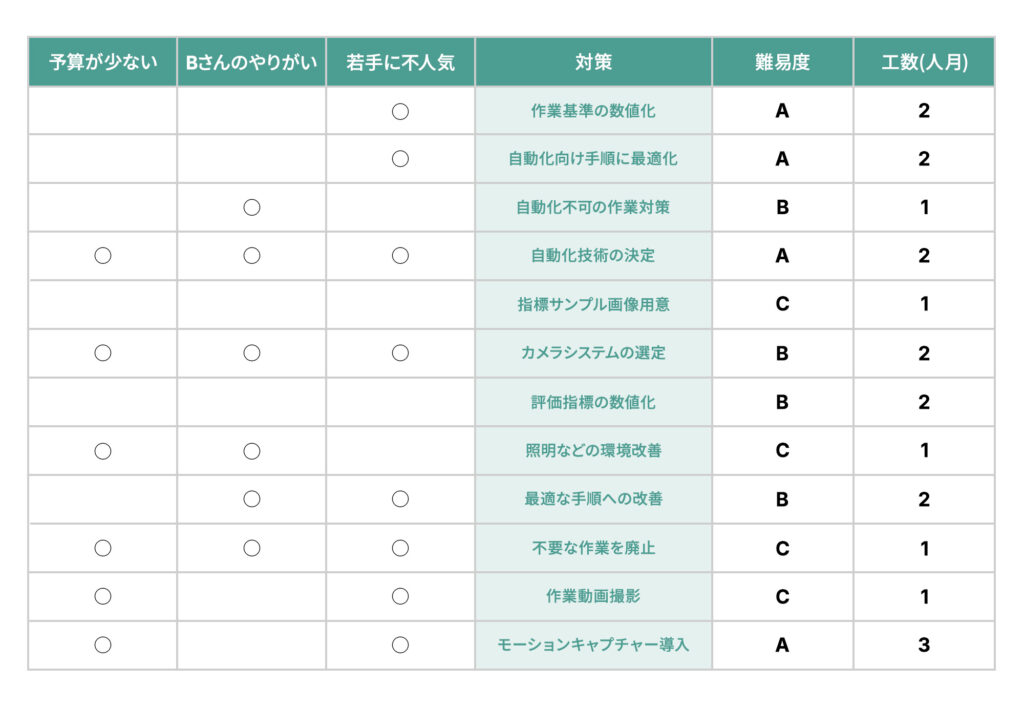
図8の左側で、原因が重複するタスクは重要度が高いと考えられます。自動化技術やカメラの選定は的確ではないと、結局、使われなくなってしまいそうです。技術選定についてはある程度専門知識が必要で、最新の動向をどれだけ的確にとらえているかも重要です。気を抜けない大切なタスクであることが分かります。
不要な作業の廃止については、多くの人にとってうれしいことなのではないかと思います。一方、分かりやすく、前向きに取り組みやすいタスクだと考えられます。
別でマトリックス図(図9)を描いて、上で決めた手段に対応する担当部署や期限を決めていくこともできます。手段の横に目的を書き出して対応の優先順位を決めた上、期限を決めていきます。
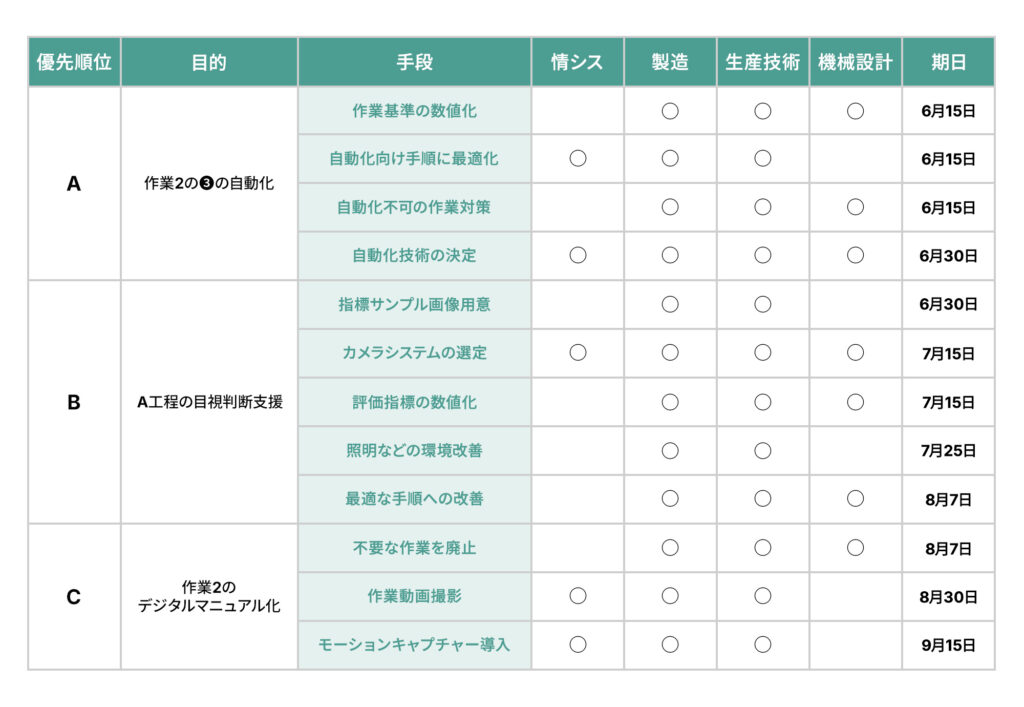
ここでは、比較的難易度が高く、手間がかかりそうな「作業2の③の自動化」をAとして対応していくとしました。DX技術の選定にはIT部門に任せきりにせず、生産工程にかかわる部署と丁寧にディスカッションしながら進められるようにします。
今回の課題が生産現場にあることから、製造と生産技術は6月から9月までDXプロジェクトにかかりきりになりそうです。例えば4部署で一緒に取り組むようなタスクであれば、両部署の負荷を減らせるように配慮する必要もあるかもしれません。
一方、設計部門はお盆休み前まで、情報システムは7月半ばからお盆休み後が比較的忙しそうです。各部署の従業員の休暇取得の計画も、このタイミングで見通しを立てることができます。
他のQCツールを助けるマトリックス図法
マトリックス図法は、多岐にわたる情報を網羅的かつ直感的に整理できます。日常生活でもよく見られる単純なL字型の図だけではなく、T字型やX字型にすることで表現できる情報の幅が広がり、より多くの情報を扱うことが可能になります。とりわけ、他のQCツールと連携して使用する事例が目立ちます。
記事一覧:【連載】「新QC&QC7つ道具」基本のキ
関連リンク:「品質管理」に関する記事一覧
参考文献
「新QC七つ道具の使い方がよ~くわかる本」(今里 健一郎・著/秀和システム・刊)
「JSQC選書26 新QC七つ道具 混沌解明・未来洞察・重点問題の設定と解決」(猪瀬正守・著/日本規格協会・刊)
「第10回 マトリックス | 10分でわかるカタカナ語 ――三省堂 ことばのコラム」(三省堂編修所)https://dictionary.sanseido-publ.co.jp/column/%E7%AC%AC10%E5%9B%9E-%E3%83%9E%E3%83%88%E3%83%AA%E3%83%83%E3%82%AF%E3%82%B9
執筆者プロフィール
facet代表 ライター、編集者。
一般社団法人 日本デジタルライターズ協会 会員。
町工場でのトレースや設計補助、メーカーでの設計製造現場での実務を経験した後、アイティメディア株式会社に入社。「MONOist」の立上げから参画し、月間100万PV以上の業界最大手サイトに成長させるべく尽力した。MONOistの編集記者として約12年間、技術解説記事の企画や執筆の他、広告企画および制作、イベント企画など、幅広く携わる。
2019年には3D設計コンサル企業の株式会社プロノハーツにジョインし、広報・マーケティング担当として従事する傍らで、製造業に特化したライティング事業を展開する。
2020年5月に個人事業として独立。
■主な執筆歴
- アイティメディア「MONOist」「TechFactory」「キーマンズネット」
- 日経BP「日経ものづくり」「日経クロステック」
- 金森産業「PlaBase」
- オートデスク「Redshift」
■書籍
- 一般社団法人セーフティグローバル推進機構
- 『実践!ウェルビーイング世界最強メソッド「ビジョン・ゼロ」』(日経BP)
- 「カーボンニュートラル 注目技術50」(日経BP、ムック)
- 「SDV革命 次世代自動車のロードマップ」(日経BP)




