関連リンク:「製造・建設に役立つツール」集
関連リンク:「図面管理」に関する記事一覧
角度計算・勾配計算ツール
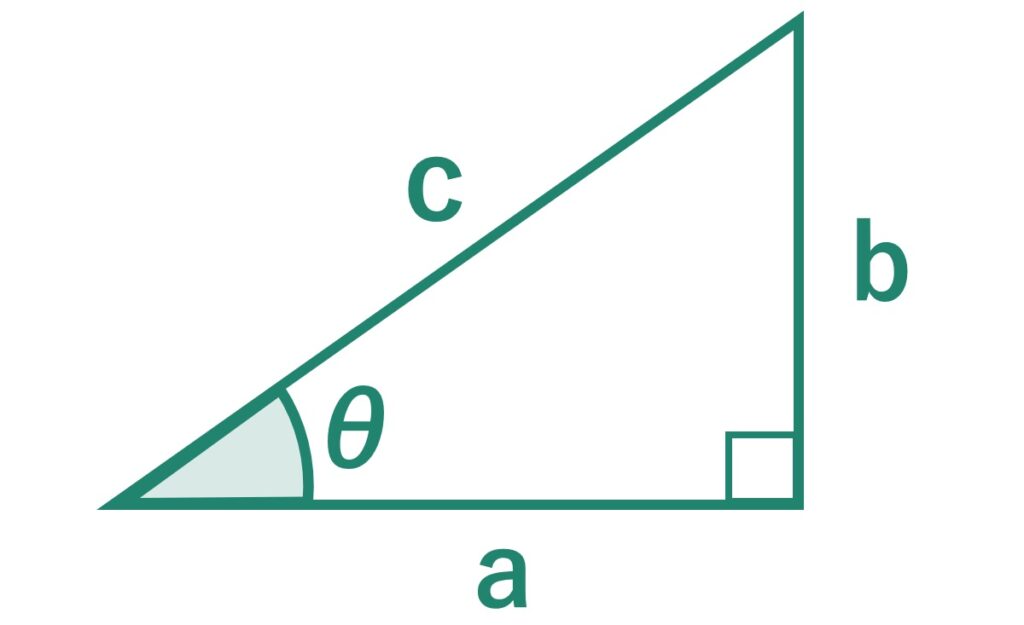
直角三角形の2辺から傾斜角度θ(勾配)と残りの1辺を求めることができます。
- 辺 ab → 角度θ(勾配)、辺 c
- 辺 ac → 角度θ(勾配)、辺 b
- 辺 bc → 角度θ(勾配)、辺 a
辺abから算出
辺acから算出
辺bcから算出
免責事項
- 本ツールに入力されたデータは、保存・計測を一切行っておりません。
- 提供する機能や結果については、十分な検証を行っておりますが、その正確性や完全性を保証するものではありません。
- 本ツールの利用により生じたいかなる損害についても、当方は一切の責任を負いかねます。
- 仕様や結果に関するお問い合わせには対応いたしかねますので、あらかじめご了承ください。
【解説】角度・勾配計算が設計・施工で重要な理由
設計図面において角度や勾配は、部品の形状・配置・加工精度、さらには建設現場での安全性や施工品質に直結する重要な要素です。しかし、角度や勾配の表記方法や単位の違いを正しく理解していないと、加工現場や施工現場との認識ズレや誤差の原因になります。
以下では、角度・勾配の単位、変換方法、計算式、三角関数の活用まで、製造業・建設業双方の実務に役立つ知識を体系的に解説します。
角度・勾配の表記方法と単位の違い
■ 弧度法(ラジアン、rad)
円の半径と同じ長さの弧がつくる中心角を1ラジアンとして角度を表す方法で、数学・物理・プログラミングで多用されます。
- 1周(360°)=2πラジアン
- 1ラジアン=57.3度
■ 度数法(deg)
円の1周を360度として角度を表す方法です。
■ 60分法(度分秒、DMS)
度数法の1度を60等分したものを1分、1分を60等分したものが1秒とする表示法です。
- 1度(°)=60分(′)
- 1分(′)=60秒(″)
例:12°20′44″ / 12度20分44秒
■ 勾配の表記(建設業)
建設業では、角度ではなく「勾配」で表すことが多く、以下の方法があります:
- 百分率 10%(垂直/水平 × 100)
- パーミル 100‰(垂直/水平 × 1000)
- 割分 1: 10(垂直1に対して水平10)
■ CAD・CAMでの注意点
- 製造業のCADでは弧度法で内部処理される場合があり、単位設定ミスが加工精度に影響します。
- 建設業の施工図では、勾配を角度に変換する場面があり、単位の確認が必須です。
角度の変換方法と計算例
■ 弧度法 θ(rad) ↔ 度数法 θ(deg) の変換
- θ(rad) = θ(deg) × π / 180
- θ(deg) = θ(rad) × 180 / π
例:π/6ラジアン → 30°
■ 度数法の小数点表記 ↔ 度分秒(DMS)変換
例:12.3456°
・度:12
・分:0.3456 × 60 = 20.736 → 20
・秒:0.736 × 60 = 44.16
→ 12°20′44.16″
例:12°20′44.16″
・整数部:12
・小数部:(20×60 + 44.16) ÷ 3600 = 0.3456
→ 12.3456°
■ 勾配 ↔ 角度
例:角度36.87° → 勾配 = tan(36.87°) ≒ 0.75(75%)
確度の計算方法と実例
■ 三角形の角度計算(余弦定理)
辺 a = 5cm、b = 7cm、c = 8cm
cos C = (a² + b² – c²) / 2ab = (25 + 49 – 64) / 70 = 0.1429
C = arccos(0.1429) ≒ 81.78°
■ 傾斜角の計算(直角三角形)
高さ = 3cm、底辺 = 4cm
tan θ = 3 / 4 → θ = arctan(0.75) ≒ 36.87°
■ 穴位置の角度計算(円周上)
円周上に等間隔で4つの穴を配置 → 各穴の中心角:360° ÷ 4 = 90°
三角関数による辺の求め方と計算例
■ 直角三角形
角度θ = 30°、隣辺 = 10cm → 対辺 = tan(30°) × 10 ≒ 5.77cm
■ 任意三角形(正弦定理)
角A = 45°、辺a = 10cm、角B = 60°
b = a × sin B / sin A = 10 × sin 60° / sin 45° ≒ 12.25cm
実務での注意点とミス防止策
- 単位の混在による誤差に注意
- CADソフトの角度設定を確認(度・ラジアン・勾配)
- 加工現場との情報共有は「単位明記」が基本
- Excelやスクリプトでの自動変換も活用可能
まとめ:角度計算・勾配計算を正しく扱うためのチェックリスト
- 単位(度・ラジアン・購買)の確認
- 三角関数の使い方を理解
- 図面と加工・施工指示の整合性をチェック
関連リンク:「製造・建設に役立つツール」集
関連リンク:「図面管理」に関する記事一覧