熱力学第二法則とは？エントロピーとエネルギー変換の仕組みを解説

【基礎】機械加工・物理法則

企画・設計

品質・保全

図面管理

CAD/3DCAD

2025.12.24

熱力学第二法則は、自然界のあらゆる現象を支配する根本的な法則の一つです。この法則は「エネルギーは保存されるが、その使える形は一方的に失われていく」という原理を示しており、発電所の効率から生命現象、さらには宇宙の運命まで、幅広い領域に影響を与えています。製造業や品質管理の現場では、熱処理プロセスや化学反応の最適化、エネルギー効率の向上といった実務課題に直結する概念でもあります。本記事では、熱力学第二法則の基本的な定義から歴史的背景、産業応用、さらには現代のエネルギー問題との関わりまで、体系的に解説していきます。

熱力学第二法則の基本定義とエントロピーの概念

熱力学第二法則は、自然界における変化の方向性を規定する根本法則です。この法則を理解する上で、まずは代表的な表現方法とエントロピーという概念を正確に把握する必要があります。

関連リンク：熱力学第一法則とは？エネルギー保存の基本をわかりやすく解説

クラウジウスとケルビンによる古典的表現

熱力学第二法則には複数の等価な表現がありますが、最も有名なのがクラウジウスとケルビンによる定式化です。クラウジウスの表現では「熱は、それ自身だけでは、低温物体から高温物体へ移ることはない」とされ、自然な熱の流れは常に高温から低温への一方向であることを示しています。一方、ケルビンの表現では「単一の熱源から熱を取り出して、それを余すところなく仕事に変え、他に何の変化も残さないような周期的機関は存在しない」とされます。

この二つの表現は一見異なるように見えますが、実は互いに導き合える等価な法則です。製造現場では、この原理がすべての熱機関の効率上限を決定する要因となります。

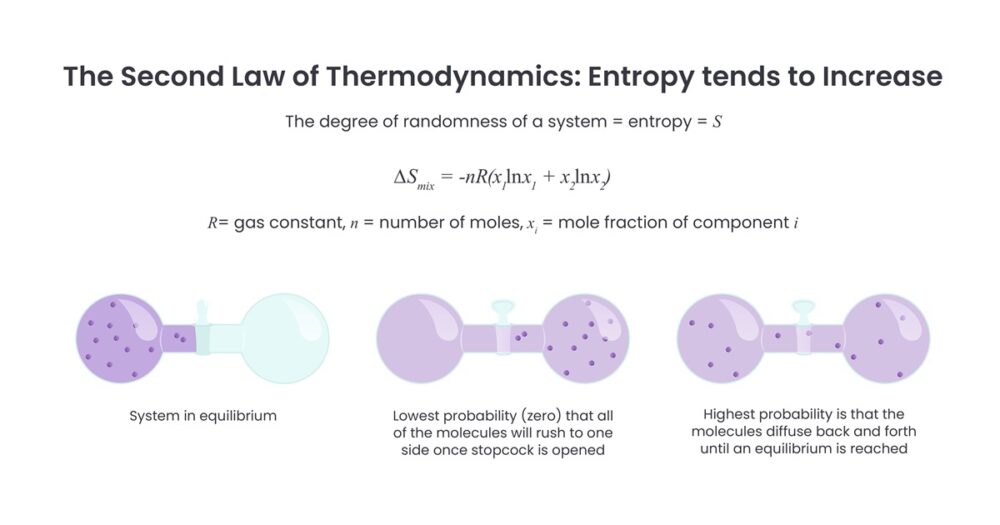
エントロピーとは何か

第二法則をより定量的に扱うために導入されるのがエントロピーという状態量です。エントロピーには二つの定義があり、マクロな視点からは可逆過程における熱量を温度で割った値として定義されます。

一方、ミクロな視点からはボルツマンの定義が重要です。エントロピーSは、系が取りうるミクロ状態数Wの自然対数にボルツマン定数kBを掛けたものとして定義されます。この定義により、エントロピーは「エネルギーの取りうる配置の数」を表す物理量となり、配置が多いほどエントロピーが大きいことを意味します。例えば、高温状態やガスの膨張状態では、分子のエネルギー配置が爆発的に増えるため、エントロピーが増大します。

エントロピー増大則と孤立系の自発変化

第二法則の最も一般的な数学表現は、孤立系においてエントロピーは増大するか、一定であるというものです。任意のサイクルについて、熱量を温度で割った値の積分は必ずゼロ以下となり、等号は可逆過程、不等号は不可逆過程に対応します。この不等式から、孤立系の自発変化では必ずエントロピーが増大することが導かれます。

エントロピーは「エネルギーの質」を表す指標でもあり、同じエネルギー量でも高温と低温の差がある状態は仕事に使いやすく、熱が均一に広がった状態では仕事に使いにくくなります。これは製造現場における熱処理や化学反応の効率評価に直結する重要な概念です。

表現方法	内容	意味
クラウジウスの表現	熱は低温から高温へ自然には流れない	熱の流れの方向性を規定
ケルビンの表現	熱を100%仕事に変える機関は不可能	熱機関の効率上限を規定
エントロピー増大則	孤立系のエントロピーは増大する	自発変化の方向性を定量的に規定

以上の表は、熱力学第二法則の三つの主要な表現をまとめたものです。これらは互いに等価であり、状況に応じて使い分けることで、さまざまな物理現象や工学的問題に適用できます。

熱力学第二法則の歴史

熱力学第二法則の発見と発展は、産業革命期の蒸気機関の改良という実用的な課題から始まりました。この過程で、エネルギーの本質と変換可能性に関する深い理解が段階的に構築されていきました。

カルノーによる熱機関理論の確立

1824年、フランスの物理学者サディ・カルノーは、蒸気機関の効率向上という実用的問題に取り組む中で、理想的な熱機関の理論を構築しました。カルノーは、熱機関が高温熱源から熱を受け取り、一部を仕事に変換して残りを低温熱源に捨てるという基本構造を分析し、その効率が熱源と冷源の温度のみによって決まることを示しました。

カルノーサイクルと呼ばれる理想的な過程は、二つの等温過程と二つの断熱過程から構成され、その効率は高温側の絶対温度Thと低温側の絶対温度Tcの比によって決定されます。この効率は任意の実在熱機関の上限となり、カルノー定理として知られています。製造現場の熱処理炉や発電プラントの設計では、この理論的上限を基準として実際の効率を評価します。

クラウジウスのエントロピー概念の導入

1850年代から1860年代にかけて、ドイツの物理学者ルドルフ・クラウジウスは、熱の流れの不可逆性を一般化し、エントロピーという新しい状態量を導入しました。クラウジウスは、熱量と温度の比から計算される量が状態量であることを示し、これをエントロピーと名付けました。

クラウジウスは「エネルギーは保存される。エントロピーは増大する」という簡潔な表現で第一法則と第二法則をまとめ、熱力学の基礎を確立しました。この定式化により、さまざまな熱機関や化学反応の効率や自発性を定量的に評価できるようになりました。

ボルツマンによる統計力学的解釈

1870年代から1900年にかけて、オーストリアの物理学者ルートヴィヒ・ボルツマンは、気体分子運動論にもとづいてエントロピーの統計的解釈を与えました。ボルツマンは、エントロピーをミクロ状態数の対数に比例する量として定義し、マクロな熱力学量とミクロな粒子の運動を結びつけました。

この統計的解釈により、第二法則は絶対的な法則ではなく、圧倒的に高い確率で成り立つ統計的法則であることが明らかになりました。マクロな系では事実上絶対的ですが、ナノスケールの系では一時的なエントロピー減少が観測される可能性があります。この視点は、現代のナノテクノロジーや量子熱力学の研究において重要な役割を果たしています。

研究者	時期	主な貢献
カルノー	1824年	理想熱機関の効率公式を導出
クラウジウス	1850-1865年	エントロピー概念の導入と定式化
ボルツマン	1870-1900年	エントロピーの統計力学的解釈
ギブズ	1870-1900年	化学平衡と自由エネルギー理論

上記の表は、熱力学第二法則の発展に貢献した主要な研究者とその業績をまとめたものです。これらの研究により、エネルギー変換の本質が徐々に明らかになり、現代の工学と科学の基礎が築かれました。

産業応用における熱力学第二法則の実践

熱力学第二法則は、製造業や品質管理の現場において、エネルギー効率の最適化や化学プロセスの設計に不可欠な理論的基盤を提供します。ここでは具体的な応用分野と実務上の考慮点を解説します。

熱機関と発電システムへの応用

すべての熱機関は、高温熱源と低温熱源の温度差を利用して仕事を取り出す装置です。火力発電所では、ボイラーで生成される高温高圧の蒸気がタービンを回転させ、発電機を駆動します。この過程において、カルノー効率が理論的上限となり、実際の効率はさまざまな損失要因によってこれより低くなります。

エネルギー効率の向上には、高温側の温度上昇、低温側の温度低下、および各種損失の低減という三つのアプローチがあり、材料技術や冷却技術の進歩が鍵となります。

化学プロセスと反応工学における自由エネルギー

化学反応の自発性と平衡状態は、ギブズ自由エネルギー変化によって判定されます。この原理は、アンモニア合成、石油精製、電池反応など、あらゆる化学プロセスの設計と最適化に適用されます。

製造現場では、反応温度と圧力の最適化が重要な課題です。反応条件を変えることでギブズ自由エネルギー変化を制御し、目的とする生成物の収率を最大化します。また、化学平衡定数と標準ギブズ自由エネルギー変化の関係を用いて、平衡組成を予測し、生産計画を立案します。

冷凍機とヒートポンプの効率評価

冷凍機やヒートポンプは、カルノーサイクルを逆に動作させることで、低温側から高温側へ熱を移動させる装置です。この過程では必ず外部から仕事を投入する必要があり、その効率は成績係数COPで評価されます。カルノー冷凍機の成績係数が理論的上限となり、実在の装置はこれより低い値となります。

工場の空調システムや冷却設備の設計では、外気温度と目標温度の差、冷媒の特性、圧縮機の効率などを総合的に考慮して、最適なシステム構成を決定します。第二法則により、温度差が大きいほど同じ冷却能力を得るために必要な仕事が増大するため、断熱性能の向上や排熱回収が重要になります。

高温熱源の温度を上げることで理論効率が向上
低温熱源の温度を下げることで理論効率が向上
摩擦損失や熱漏れなどの不可逆要因を低減
排熱を有効利用するコジェネレーションシステムの導入
材料技術の進歩による高温動作の実現

上記のリストは、熱機関の効率を向上させるための主要なアプローチをまとめたものです。これらの方策は、第二法則の制約の中で最大限の性能を引き出すための実践的な指針となります。

エネルギー利用における制約と機会

熱力学第二法則は、エネルギー変換に本質的な制約を課す一方で、この制約を理解することで新たな技術開発の機会も生まれます。ここでは、リスクと機会の両面から考察します。

エネルギー変換効率の絶対的上限

第二法則により、あらゆる熱機関には効率の絶対的上限が存在します。発電所、内燃機関、ガスタービンなど、すべての熱機器はカルノー効率を超えることができません。この制約は、技術がどれほど進歩しても原理的に変わることはありません。

製造現場では、この理論的上限を基準として実際の装置の性能を評価し、改善の余地を定量的に把握することが重要です。現状の効率がカルノー効率に近い場合、さらなる効率向上は極めて困難であり、システム全体の最適化や排熱利用などの別のアプローチが必要になります。

廃熱と環境負荷のトレードオフ

第二法則により、エネルギー利用には必ず廃熱が伴います。発電所では投入エネルギーの半分以上が冷却水や排気ガスとして環境に放出され、大規模エネルギー利用は周辺の環境温度や生態系に影響を及ぼします。製造現場における熱処理プロセスでも、同様の課題が存在します。

廃熱を最小化するには、プロセス温度の最適化、断熱性能の向上、排熱回収システムの導入などが有効です。また、廃熱を他のプロセスで利用するカスケード利用や、温水供給に活用する地域熱供給システムなど、エネルギーの多段階利用が持続可能なエネルギー管理の鍵となります。

非平衡系における秩序形成の可能性

第二法則は孤立系でのエントロピー増大を述べますが、外部とエネルギーをやり取りする開放系では、局所的な秩序形成が可能です。生命現象はその典型例であり、太陽からのエネルギー流入を利用して高度な秩序構造を維持しながら、環境へのエントロピー排出を通じて全体のエントロピーを増大させています。

この原理は、材料プロセスにおける自己組織化や、化学反応における周期的パターン形成などに応用されています。非平衡熱力学の理論により、エネルギー流を適切に制御することで、所望の構造や機能を持つ材料を効率的に生成できる可能性が広がっています。

リスク・制約	機会・対策
熱機関の効率に絶対的上限が存在	理論限界を基準とした性能評価と最適化
エネルギー利用に必ず廃熱が伴う	排熱回収とカスケード利用の推進
大規模利用による環境への影響	省エネ技術と再生可能エネルギーの導入
不可逆過程によるエネルギー散逸	プロセス設計の改善と損失低減

この表は、熱力学第二法則がもたらす制約と、それに対応する技術的機会をまとめたものです。制約を正確に理解することで、効果的な対策を講じることが可能になります。

まとめ

熱力学第二法則は、エネルギーの総量は保存されるものの、その利用可能な形態は一方的に失われていくという自然界の根本原理を示しています。クラウジウスとケルビンによる古典的表現から、エントロピー増大則、さらにはボルツマンの統計的解釈まで、複数の視点から理解することで、この法則の意味が明らかになります。

製造業や品質管理の現場では、熱機関の効率評価、化学反応の自発性判定、冷却システムの設計など、幅広い実務課題に第二法則が適用されます。カルノー効率が示す理論的上限を基準として、実際のプロセスの改善余地を定量的に評価し、排熱回収やカスケード利用などの実践的対策を講じることが、持続可能なエネルギー管理において大切です。第一法則との相補的関係や自由エネルギー概念との連携により、エネルギーの量と質の両面から総合的な評価が可能になります。熱力学第二法則を正しく理解することは、現代の製造プロセスを支えることにつながるでしょう。

関連リンク：熱力学第一法則とは？エネルギー保存の基本をわかりやすく解説