熱力学第一法則とは？エネルギー保存の基本をわかりやすく解説

関連リンク：「機械加工・物理法則」に関する記事一覧
関連リンク：「図面管理」に関する記事一覧

熱力学第一法則の基本的な定義と数学的表現

熱力学第一法則は、エネルギー保存の法則を熱現象に適用した形で表現されており、物理学や化学、工学の基礎として位置づけられています。まずはこの法則の基本的な定義と数学的な表現方法について理解していきましょう。

関連リンク：熱力学第二法則とは？エントロピーとエネルギー変換の仕組みを解説

熱力学第一法則の定義と本質

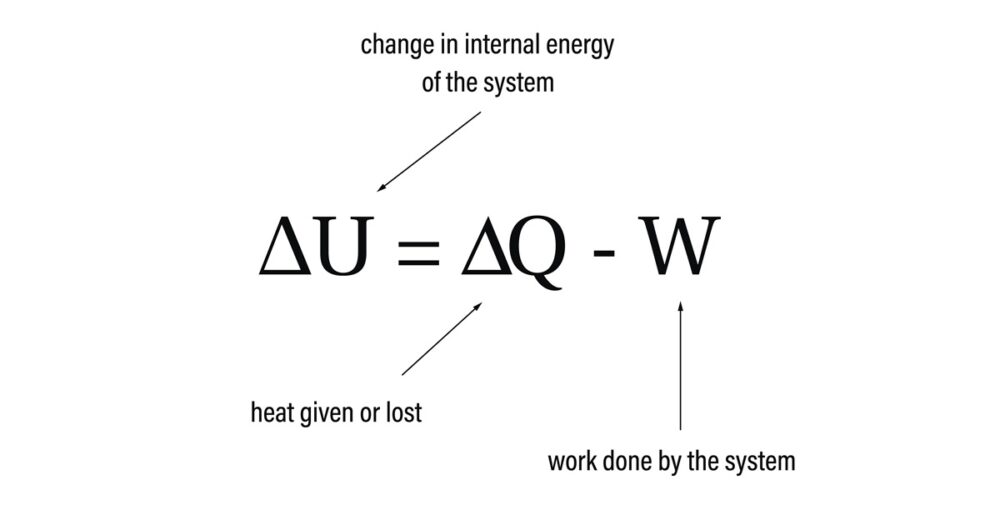
熱力学第一法則は「系の内部エネルギーの増加は、外界から系が受け取った熱量から、系が外界にした仕事を差し引いたものである」と定義されます。これはエネルギーが形を変えて出入りしても、全体としては増減しないというエネルギー保存の原理を、熱や仕事を通じたエネルギー収支の形で定式化したものです。

この法則の本質は、エネルギー保存則が熱現象や熱力学系に適用された特別な形であるという点にあります。別の言い方をすれば、第一種永久機関は不可能であるということを意味しており、外界からエネルギーを受け取らずに無限に仕事をし続ける装置は作れないことを示しています。この原理は産業革命時代の蒸気機関の研究から発展し、現代のあらゆるエネルギー変換技術の基盤となっているのです。

数学的表現と記号の取り扱い

熱力学第一法則の数学的表現には、記号の取り方によって異なる形が存在します。物理学や化学のテキストでよく用いられる形は次のようになります。

ΔU = Q – W

ここで、ΔUは内部エネルギーの変化、Qは系が外界から吸収した熱量（吸熱を正とする）、Wは系が外界に対してした仕事（膨張仕事など、対外仕事を正とする）を表しています。一方、化学熱力学系統の一部では、ΔU = Q + W という形を採用し、Wを「外界が系にした仕事（圧縮など）」として正にとる約束もあります。このような記号規約の違いは、工学系と化学系で慣習が異なるため、実務や教育の現場で混乱が起きやすい点として注意が必要です。

構成要素としての系と周囲

熱力学第一法則を理解する上で重要なのが、系（system）と周囲（surroundings）の概念です。系とは考察対象となる物体や物質、装置の集合を指し、周囲とは系以外のすべてを意味します。系と周囲を合わせたものを宇宙（孤立系）とみなしたとき、そのエネルギーは一定に保たれます。

内部エネルギーUは、系を構成する粒子の運動エネルギー（並進・回転・振動）と相互作用ポテンシャルエネルギーなどを含む総エネルギーであり、状態関数として定義されます。状態関数とは、始状態と終状態だけで決まり、その間の経路に依存しない量のことです。一方、熱Qと仕事Wは経路量であり、プロセスのとり方によって値が変わる点が大きな違いとなります。

熱と仕事の定義と区別

熱Qは、温度差を駆動力として統計的な粒子運動の乱雑さをともなうエネルギー移動形態です。これに対して仕事Wは、規則的な力学的運動や電場などを通じた秩序あるエネルギー移動形態として定義されます。熱と仕事の区別は、境界条件の取り方によって分類が変わることもあり、境界の概念を重視する立場と統計力学的定義を重視する立場が存在します。この区別を正確に理解することは、実際のエネルギー収支計算において極めて重要となります。

項目	内部エネルギーU	熱Q	仕事W
性質	状態関数	経路量	経路量
経路依存性	なし	あり	あり
エネルギー移動の特徴	系全体の総エネルギー	温度差による乱雑な移動	力学的な秩序ある移動
測定方法	間接的に算出	カロリメトリー	力×距離など

熱力学第一法則の歴史

熱力学第一法則の成立には、産業革命における蒸気機関の発展と、19世紀の科学者たちによる熱と仕事の関係性の解明という歴史があります。ここでは、この法則がどのように確立されてきたのかを見ていきましょう。

産業革命と蒸気機関の役割

18世紀から19世紀にかけての産業革命において、蒸気機関は製造業の動力源として急速に普及しました。この時期、蒸気機関の効率向上が重要な技術課題となり、「熱は仕事にどのように変わるか」「どこまで効率を上げられるか」という問題意識が生じました。

これらの実践的な問題を解決するために、熱と仕事の関係が体系的に調べられるようになりました。当初、熱は「カロリック」と呼ばれる流体のようなものと考えられていましたが、機械的仕事と熱が定量的に変換可能であることが次第に明らかになっていったのです。

主要な研究者による貢献

熱力学第一法則の確立には、マイヤー、ジュール、グローブといった科学者たちの研究が大きく貢献しました。マイヤーは熱と仕事の等価性の観念的理解を進め、エネルギー保存の考え方を早期に提示したとされています。

特に重要なのがジュールによる実験的研究です。彼は1840年から1848年にかけて一連の精密な実験を行い、機械的仕事と熱量の定量的関係を高精度で測定しました。これにより、熱の仕事当量（1 cal ≒ 4.184 J）が与えられ、エネルギー保存の実験的基盤が築かれました。また、グローブは熱・電気・光など各種エネルギー形態の相互転換の観念をまとめ、これらの成果が統合されて1850年前後に熱力学第一法則として明確に定式化されていきました。

現代における位置づけと発展

確立から170年以上が経過した現在でも、熱力学第一法則は古典熱力学だけでなく、統計力学や量子論におけるエネルギー概念の基礎として有効性を保っています。この法則は、発電・冷凍・空調・自動車・化学プロセスなど、あらゆるエネルギー機器の設計・評価の基本式として使われています。

教育面では、物理学・化学・工学系の基礎科目として世界的に標準化された内容になっており、熱力学四法則のうちの中心的位置を占めています。さらに近年では、エネルギー政策や環境問題の基礎としても重要性が増しており、再生可能エネルギーの導入や省エネルギー設計の必要性を定量的に裏づける枠組みとして機能しています。

熱力学第一法則の産業応用と実践事例

熱力学第一法則は理論にとどまらず、製造業や工場現場における様々なエネルギー変換プロセスの基盤となっています。ここでは具体的な応用分野と実践的な事例について解説していきます。

熱機関と発電プラントへの応用

発電所や内燃機関などの熱機関では、燃料の化学エネルギーが熱に変換され、さらに機械的仕事を経て電気エネルギーへと変換されます。この一連の変換プロセスの収支を第一法則で記述することで、設備効率の評価や改善が可能になります。

大規模な発電プラントでは、わずか数パーセントの効率改善でも年間数億円規模のコスト削減につながるため、この分析は極めて重要です。

冷凍機とヒートポンプの設計原理

冷凍機やヒートポンプは、熱機関とは逆に外部から仕事を投入して熱を移動させる装置です。これらの装置では、外部から仕事Wを投入し、低温熱源から熱QLを吸収して高温熱源にQHを放出します。

製造現場では、冷凍設備や空調設備の運転コストが大きな割合を占めることも多く、第一法則にもとづくエネルギー収支分析により、最適な運転条件の設定や設備更新の判断材料を得ることができます。特に食品工場や化学プラントでは、温度管理が品質に直結するため、精密なエネルギーバランス管理が求められます。

化学プロセスにおける熱収支管理

化学反応をともなうプロセスでは、反応熱、相転移熱、溶解熱などを正確に把握することが製品品質と安全性の確保に不可欠です。大規模な化学プラントでは、複数の反応器や熱交換器が連結されており、全体のエネルギーフローを第一法則にもとづいて最適化することで、エネルギー原単位の削減と生産性の向上を同時に実現できます。また、異常な発熱や吸熱は事故の予兆となる場合もあるため、リアルタイムでのエネルギー収支監視は安全管理の観点からも重要です。

応用分野	主なエネルギー変換	第一法則の活用方法	管理上の重点
発電プラント	化学→熱→機械→電気	入出力エネルギー収支の定量化	総合効率の向上、損失箇所の特定
冷凍・空調	電気→機械→熱移動	COP評価と最適運転条件の設定	運転コスト削減、温度管理精度
化学プロセス	化学反応にともなう熱収支	反応熱の測定と熱交換設計	品質管理、安全性確保
内燃機関	化学→熱→機械	燃焼効率と排熱損失の分析	燃費向上、排出ガス低減

熱力学第一法則と第二法則の関係性

熱力学第一法則を正しく理解し実務に活用するには、第二法則との関係性を把握することが不可欠です。両者は相互補完的な役割を果たしており、エネルギー変換プロセスの完全な理解には両方の視点が必要となります。

量的保存と質的制約の違い

熱力学第一法則はエネルギーの「量」が保存されることを示していますが、そのエネルギーをどのように利用できるかという「質」については何も語っていません。この質的側面を扱うのが第二法則であり、自然過程の不可逆性とエントロピー増大の原理を規定しています。

第一法則だけではどのような過程が自然に起こるか、なぜ時間には向きがあるのかを説明できず、第二法則と組み合わせて初めて現実の過程を制約できます。たとえば、高温物体と低温物体を接触させたとき、熱は高温側から低温側へ自然に流れますが、その逆は起こりません。この方向性は第一法則だけでは説明できず、第二法則のエントロピー増大則によって理解されます。

熱機関の効率限界とカルノーサイクル

熱機関の効率を考える際、第一法則により入力エネルギーと出力エネルギーの収支は把握できますが、理論的な効率の上限を決定するのは第二法則です。カルノーサイクルは、高温熱源と低温熱源の間で動作する熱機関の理論的最高効率を与えるものであり、この効率は温度だけで決まり、作動物質によらないことが示されています。

実際のエンジンや発電設備の効率がカルノー効率に達しないのは、摩擦や熱損失、不完全燃焼などの不可逆過程が存在するためです。第一法則でエネルギー収支を管理しつつ、第二法則で理論限界を認識することで、改善余地の現実的な評価が可能になります。

エクセルギーと有効エネルギーの概念

第一法則と第二法則を統合した概念として、エクセルギー（有効エネルギー）があります。エクセルギーとは、与えられた環境条件のもとで理論的に取り出せる最大の仕事量を表す指標です。第一法則はエネルギーの総量を扱いますが、エクセルギー解析は仕事に変換可能な部分、つまりエネルギーの質を評価します。

製造現場では、エネルギー消費量だけでなく、エクセルギー効率を指標とすることで、より本質的な省エネルギー対策を立案できます。たとえば、高温の排熱を単に捨てるのではなく、発電や他のプロセスの予熱に利用することで、エクセルギー損失を削減できます。

実務における注意点とリスク管理

熱力学第一法則を実務に適用する際には、いくつかの注意点とリスクを理解しておく必要があります。理論を正しく現場に適用し、誤用を避けるための実践的なポイントを解説します。

系の定義と境界設定の重要性

エネルギー収支計算において最も重要なのが、系の定義と境界の明確な設定です。系の定義が曖昧なままエネルギーバランスをとると、エネルギーが「消えた」あるいは「増えた」ように見える誤解が生じます。

実際の工場やプラントでは、配管放熱、摩擦損失、漏れなど計測範囲外の損失を過小評価してエネルギーバランスが合わないケースが頻繁に発生します。このような場合、系の境界を見直し、見落としていた熱損失や仕事の項目を再評価する必要があります。特に大規模システムでは、測定点を増やし、区画ごとに詳細な収支を取ることで、損失箇所を特定できます。

測定精度と誤差の管理

エネルギー収支分析の精度は、温度・圧力・流量などの測定精度に大きく依存します。センサーの校正不良や経年劣化により、測定値に系統的な誤差が含まれると、エネルギー収支が数パーセント以上ずれることもあります。

定期的な計器の校正と、複数の測定手法による相互検証が重要です。また、エネルギー収支の不均衡が許容範囲を超えた場合、測定系の異常か実際のプロセス異常かを判断するプロトコルを整備しておくことが、品質管理と安全管理の両面で重要となります。

以下の表を参考に、適切なリスク対策を実施しましょう。

リスク項目	具体的な問題	対策方法
系の定義不明確	エネルギー収支の不一致	境界を明確化し、損失項目を網羅的に把握
測定誤差	分析精度の低下	定期校正と複数手法による検証
擬似科学の混入	非現実的技術への投資	熱力学専門家による技術評価
適用範囲の誤用	理論の不適切な外挿	前提条件と限界の明確化

まとめ

熱力学第一法則は、エネルギーが形を変えても総量は保存されるという基本原理を示しており、製造業における全てのエネルギー変換プロセスの基盤となっています。系の内部エネルギー変化は、外界から受け取った熱量と系が外界にした仕事の差として表現され、この関係式を用いることで発電プラント、冷凍機、化学プロセスなどの設計と効率評価が可能になります。

第一法則はエネルギーの量的保存を扱いますが、実際のエネルギー変換の方向性や効率限界を理解するには第二法則との併用が不可欠です。両者を統合することで、理論的な効率上限を認識しつつ現実的な改善策を立案できます。

実務では系の境界を明確に定義し、測定精度を管理することで、エネルギー収支分析の信頼性を確保できます。 大企業の製造現場や工場管理においては、熱力学第一法則にもとづくエネルギー管理が省エネルギー施策の定量的評価や設備投資判断の科学的根拠となります。この基本原理を正しく理解し適用することで、持続可能な生産システムの構築とコスト競争力の強化を実現できるでしょう。

関連リンク：熱力学第二法則とは？エントロピーとエネルギー変換の仕組みを解説

関連リンク：「機械加工・物理法則」に関する記事一覧
関連リンク：「図面管理」に関する記事一覧