ゲージR&Rを計算してみよう｜熊野コミチの「ものづくり統計学」【第6回】

みなさん、こんにちは。熊野コミチです。

モノづくりのための統計学、第６回は「ゲージR&R」について解説いたします。

ゲージR&R（以下GR&R)は、測定システムの信頼性を統計的に検証するための手法です。顧客側から「おたくの測定システム、ホンマに大丈夫？」って感じで要求されることが多いです。ただこの手法要求されることが多い割には、詳しい解説が出回っていないんですよね。特に計算方法については、「平均-範囲法」というものが主に出回っているのですが、これが管理図の管理限界線の計算で使われるような謎の係数が使われていることもあって、いまいち何を計算したいのか分かりづらいんです。

ということで今回はGR&Rの概要、ANOVA法、使用における実態について解説いたします。

GR&Rの概要

GR&Rは測定システム分析(MSA)という手法の一つで、ゲージの繰り返し性(Repeatability)と再現性(Reproducibility)という、以下の２つのばらつきを分析する手法です。

• 繰り返し性：測定器によるばらつき
• 再現性：測定者によるばらつき

測定によるばらつきというのは、サンプル間のばらつき、測定器によるばらつき、測定者によるばらつきの累積によって成り立っています。故に良い測定システムというのは、サンプル間のばらつきだけが際立ち、相対的に測定器や測定者によるばらつきが小さいシステムを指すのです。

重要なのは、“測定システム”の評価であるという事。つまり校正で測定器そのものが問題ないと確認されても測定システムという目線で評価した場合に不合格になる可能性があるんです。

例えばシックネスゲージ。こちらの校正を行う場合は、金属でできたゲージブロックで行います。それで、問題がなかったとしましょう。

しかしPETフィルムを測る測定器としては適当かと言われたら、そうとも限らないのです。PETは金属と異なり柔らかいため、シックネスゲージの圧力による変形や人による当て方、傾きで本来の厚みが測定されない可能性があります。つまりPETフィルムを測る”システム”としては不適である可能性が出てくるわけです。

「校正はしてるけど、なんかこの測定器信用できないんだよなぁ」って場合は、この測定システム目線で検証すれば問題点をあぶりだせます。繰り返し性が悪い場合は、測定器そのものを別のものに変更しないといけないし、再現性が悪い場合は測定者への再教育が必要になります。

顧客側からしても校正記録を見せられるよりもよほど実態に迫った調査が出来るので、GR&Rを要求するのも当然っちゃ当然なんですよね。

昔FT-IRの測定結果がやたら測定者によって違う気がするって状況に直面しまして、試しにGR&Rで検証すると、見事に再現性だけがめちゃくちゃだった事がありました。再現性だったので、再教育をすることで安定するようになり、買い替えなどの過剰なコストが発生せずにほっとした記憶があります。

GR&Rの計算法

GR&Rの計算方法ですが、一般的には平均-範囲法で計算されることが多い印象です(昔受けたIATFの研修や、顧客から要求された場合に提供されたフォーマットなど)。

ですが、平均-範囲法だとGR&Rの本質がつかみにくいです。また特殊な係数が使われるのですが、その係数が繰り返し数や測定人数が3までしか準備されておらず、他の測定人数5人いるんだけどみたいな状況に対応できないのです。

ですので、私は分散分析を応用したANOVA法を推奨しています。計算が難しいし、分散分析難しいって感じでそりゃ避けられるよねというのも、とても分かるのですが、それでもばらつきの足し算、引き算というGR&Rの本質をつかみやすいのはこのANOVA法なんですよね。

まぁ計算とか面倒、フォーマットがあるから興味ないという方は、ここの項目は読み飛ばしちゃってください。

表1の数値群を使って計算してみましょう。

まず分散分析表を作ってみます。分散分析についての詳細は、記事末で紹介している私のYouTubeチャンネルを確認してみてください。

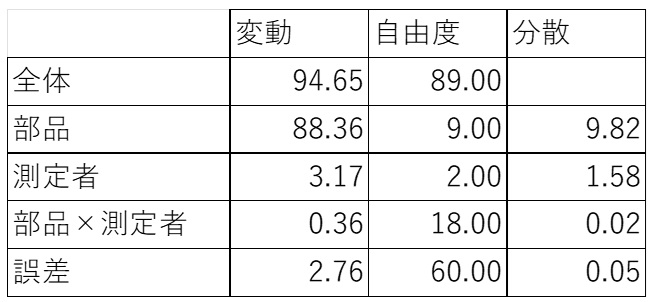
表2の分散に注目です。まず一番下の誤差というのは、部品でも測定者でも、その交互作用(部品×測定者)にも該当しません。つまり必然的に測定器の分散に該当します。

ここから出すGR&R関係の値は分散の平方根、つまり標準偏差に該当しますので、この誤差（測定器)の分散の平方根が測定器のばらつき（EV)になります。

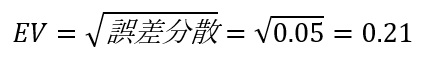
次に測定者のばらつき（AV)です。測定者の分散値には誤差の分散が含まれているので、まずはそれを引きます。そして一測定分のばらつきにするために部品数（10)×測定回数(3)=30で割り、その平方根を算出します。

部品のばらつき（PV)もAVと同じです。部品の分散値に誤差の分散が含まれているので、まずはそれを引きます。一測定分のばらつきにするために、測定者(3)×測定回数(3)=9で割り、その平方根を算出します。

そしてGR&Rですが、これはEVとAVの二乗平均平方根を計算します。

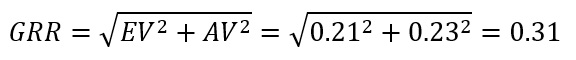
トータルを示すTVはEV,AV,PVの二乗平均平方根を計算します。

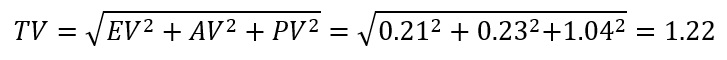
そして最後にGR&Rの全変動を算出します。GR&RをTVで割ります。

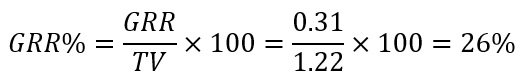
各要素の全変動も出す表3のようになります。

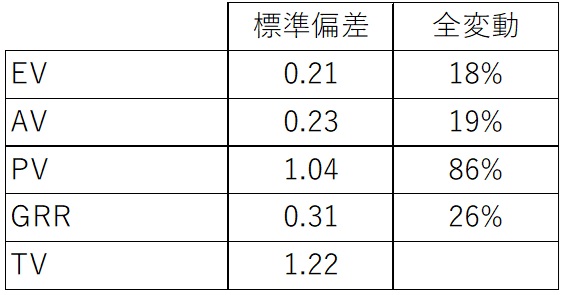
ここでGRRの%が、

• 10%以下なら合格
• 10%～30%以下なら条件付き合格
• 30%より大きいなら不合格

となります。

今回の場合は26%なので、ぎりぎり合格といったところです。

そしてGR&Rを構成するEVとAVのうち、いずれも同じくらいの値なので、どちらが悪いのではなく、全体的に安定させる必要があるという結果になります。コスト的には測定者ばらつきを抑えたいところですが、おそらくそれでは10%以下にはならなさそうですね。

いきなり監査で「GR&Rの結果を見せてください」と言われたら？

このGR&Rを使えば統計的に測定システムの評価が出来ます。ですが、この評価法を実用したことがある方はご存じかもしれませんが、問題点があります。それが”合格しない”という点です。GR&Rが10%以下にならないのですよ。肌感では問題なさそうな測定システムであっても、中々合格しないんです。

それはなぜかというと、適度にばらついたサンプルを選ぶことが難しいからです。GR&Rは人、測定器のばらつきがサンプルそのものに対してきわめて小さいかという”相対的な評価法”です。つまり準備したサンプルが全て平均値付近のものである場合、実用的には問題ない測定システムであっても不合格になってしまう可能性があるんです。これが結構問題でして、例えば他社からの監査があり、「GR&Rの結果を見せてください」といきなり言われた場合、適当にサンプリングしても不合格になってしまう可能性があるんです。

また社内の取り組みで検証する場合でも、普段実用する上では問題ない測定システムを不合格にしてしまって、対策に追われるという結果になる可能性もあります。

これらの問題を解消するためには、規格幅に対するGR&Rの評価を示すことが有効です。これを式で表すと、このようになります。

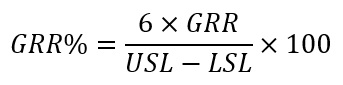
これが10%以下になった場合、測定サンプルの規格幅を評価する上では十分な能力を有している事を示すことが出来ます。ちなみに6という数字は測定システムのばらつきが正規分布すると仮定して、±3σ分ずれることから来ています(工程能力指数の逆数をイメージするとわかりやすいです)。例えば、先ほどのデータを例にして、規格幅が20だとします。この場合、

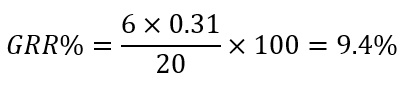
で合格となります。

ちなみにこれが規格幅10の場合、こうなります。

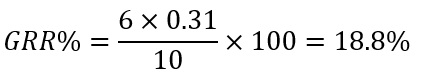
条件付き合格です。

従来の手法の場合はサンプルが十分にばらついていないといけないので、工程の改善が進むほどに実態として十分な能力を有していたとしても、サンプルがばらつかなくなるので不合格になりやすくなります。監査に合格するためにわざとサンプルをばらつかせる必要が出てきます。全く無駄な労力です。一方で規格幅を対象とすると、サンプルのばらつきが小さくなっても、関係ありません。いきなり監査に来られてもランダムにサンプリングして正しく測定システムを示すことが出来ます。逆に監査する側になった場合も同様でこちらからランダムにサンプルを選んで公平な評価をすることが可能となります。

また、GR&Rそのものでは、数値で測定システムの評価が見えるかできますが、その数字がピンとこないのでどこをどう是正したらいいのかが分かりづらいという問題もあります。

その場合は測定データをグラフ表記すると分かりやすいです。例えば人別で箱ひげ図を描くと、この通りです。

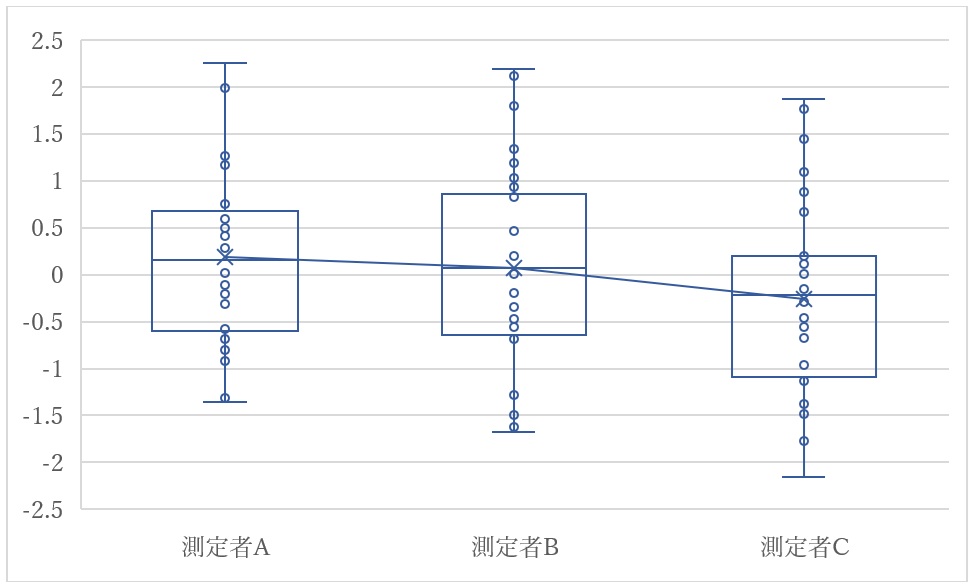
人別でばらつきに違いはないけれど、測定者Cは他の人に比べて低めの値を出しがちということが一目で分かります。ですので測定者Cの測定方法をヒアリングしたり、再教育したりすることで、AVの改善が出来る可能性が出てきます。

GR&Rは監査で頻繁に用いられる割には、その実態に謎が多い手法です。日本語の文献が乏しいのが原因みたいですね。その上、一般的には平均-範囲法による評価が出回っているので、数学的に何をしているのか分かりづらいですね。

分散分析をもとにした二元配置分散分析（ANOVA）であれば、ちょっと難しいですが、数学的には納得いただきやすいと思います。

私のYouTubeチャンネルでも、分散分析の解説をしております。ぜひ併せて見てみてください。

関連リンク：分散分析を数式を使わず分かりやすく解説します｜統計とお仕事チャンネル（YouTube）関連リンク：一元配置分散分析で要因の効果を分析しよう 開発でめっちゃ使えます｜統計とお仕事チャンネル（YouTube）

またGR&Rについての日本語文献としては、「管理図・SPC・MSA入門: JUSE-StatWorksオフィシャルテキスト 」にANOVA法の計算方法も載っておりお勧めです（日本語の本で解説があるのをあまり見たことがないように思います)。

参考文献
管理図・SPC・MSA入門: JUSE-StatWorksオフィシャルテキスト 
（奥原 正夫 ・加瀬 三千雄 著、日科技連出版社・刊）

記事一覧：【連載】熊野コミチの「ものづくり統計学」

---

執筆者プロフィール